Turing Machines

A Turing machine (TM) is a foundational computational model, with capabilities equivalent to most general-purpose computing devices. It defines the same set of computable functions.

There are two main types of Turing machines, distinguished by their handling of state transitions.

• Deterministic Turing Machine (DTM)
  A DTM operates under strict rules: for each state and symbol read by the head, there is exactly one possible action the machine can take, whether it’s moving the head, writing a symbol, or switching states.
• Non-deterministic Turing Machine (NDTM)
  An NDTM, in contrast, can choose from multiple possible actions for each state-symbol pair it reads. This means that from any given configuration, the NDTM can “choose” among different potential transitions.

  This endows it with a kind of "predictive power," enabling it theoretically to explore multiple computational paths simultaneously, which can significantly speed up the processing time for certain problems.

Deterministic Turing Machines

Deterministic Turing machines (DTM) are a specialized category of TM that function according to predefined rules.

Each DTM is equipped with a control unit that manages state transitions and an infinite tape divided into cells, each capable of holding a symbol from a predefined set.

The read/write head of the machine interacts with this tape, reading and writing symbols as it moves horizontally in accordance with the program’s directives.

Key operations of a DTM include reading and writing symbols on the current cell, moving the head, and altering the state of the control unit based on both the symbol read and the current state.

A TM is defined by a finite set of states, an initial state, acceptance states that indicate successful input processing, readable input symbols, and a larger set of writable tape symbols, including the blank symbol for empty cells.

These characteristics establish TMs and DTMs as universal models within the field of computing.

Example

Consider a Turing Machine (TM) designed to solve a straightforward task: determining whether a binary string has an even number of 1s.

We will explore a deterministic version of this machine.

The machine utilizes an infinite tape, starting with the provided binary string, while all other spaces are marked with blank symbols (denoted as B).

States:

• q0: The initial state.
• q1: Indicates an odd running count of 1s.
• q_accept: An acceptance state, reached when the string ends with an even count of 1s.
• q_reject: A rejection state, reached when the string ends with an odd count of 1s.

Transitions:

• From q0 to q0: Reads 0, writes 0, moves right.
• From q0 to q1: Reads 1, writes 1, moves right.
• From q1 to q0: Reads 1, writes 1, moves right.
• From q1 to q1: Reads 0, writes 0, moves right.
• From q0 to q_accept: Reads B (blank, signaling the end of the string), moves right.
• From q1 to q_reject: Reads B, moves right.

Let's illustrate with the string "1101" and trace the machine’s operations:

1. Starting state is q0.
2. Starts in q0, reads 1 - transitions to q1, writes 1, moves right.
3. In q1, reads 1 - transitions back to q0, writes 1, moves right.
4. In q0, reads 0 - remains in q0 , writes 0, moves right.
5. In q0, reads 1 - transitions to q1, writes 1, moves right.
6. In q1, reads B - moves to q_reject, as the final count of 1s is odd.

This demonstration shows how a Deterministic Turing Machine processes a string to determine whether the count of 1s is even or odd, concluding in an acceptance or rejection state based on this count.

We can visually represent a Turing Machine’s workings, like the example shown, with a state diagram that outlines the states of the machine and the transitions between them.

Here is the visual representation:

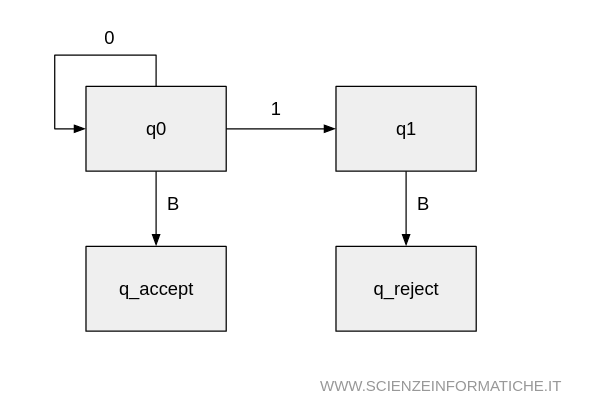
The blocks q0 and q1 are states used to track the count of 1s in the string, with q0 for an even count and q1 for an odd count.

The arrows indicate transitions between states, each labeled with the symbol read by the head. In this simplified diagram, assume that the symbol written is identical to the one read and the head always moves right.

The q_accept and q_reject states are the terminal states that determine the machine’s outcome based on the parity of the 1 count at the end of the string.

This graphical layout aids in visualizing how the Turing Machine processes an input string