Linear Regression Explained
Regression analysis is a cornerstone statistical technique, essential for predicting a continuous variable based on known factors. Take, for example, the estimation of a house's price, which can be determined by considering various aspects such as size and location.
Understanding Linear Regression
Linear regression stands out as one of the most widely-utilized techniques in regression analysis.
This approach posits a straightforward linear relationship between an independent variable X (like the size of a house) and a dependent variable Y (such as the price of the house).
The formula that represents this relationship is:
$$ Y =a⋅X+b $$
Breaking it down:
- f(Y) is the estimated value of Y, which in our example, would be the house price.
- "a" denotes the coefficient of the independent variable, reflecting how much Y alters in response to a unit change in X.
- "b" represents the intercept, the value of Y when X equals zero.
In the training phase of a linear regression model, the prime objective is to ascertain the optimal values of "a" and "b". Here, "a" is the line's slope, and "b" its intercept.
The end goal? To discover the line, defined by the formula Y=aX+b, that aligns most closely with the training data.
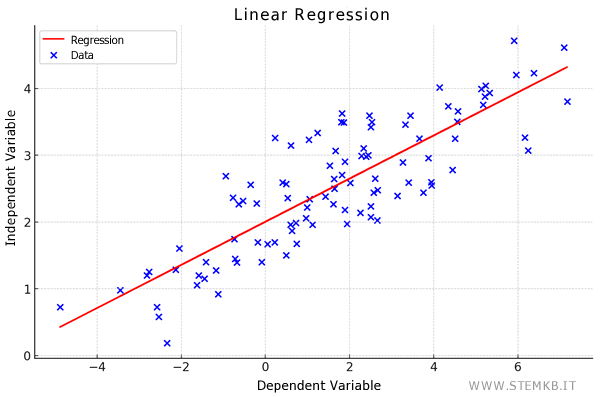
This is typically achieved by minimizing a cost function, which quantifies the discrepancy between the predicted values of the model and the actual training data.
A pivotal metric in linear regression is the coefficient of determination, better known as R2. This indicator, which fluctuates between 0 and 1, reveals the extent to which the model corresponds with the data. An R2 nearing 1 indicates a model that aptly explains the data variability, whereas a value approaching 0 suggests the opposite.
It's important to note that linear regression with a solitary variable might struggle to encapsulate complex nonlinear relationships due to its inherent assumption of a linear connection between the independent and dependent variables.
This phenomenon, known as underfitting in machine learning, can hinder the model's effectiveness.
Moreover, the accuracy of predictions can be compromised in the presence of significant data variability or outliers. These outliers can warp the regression line, given its sensitivity to such anomalous data points.
Outliers, in data analysis, refer to observations that markedly deviate from the majority.
Multiple Linear Regression
Multiple linear regression is an enhanced variant that incorporates several independent variables. This model takes the form:
$$ f(Y)=a_1⋅X_1+a_2⋅X_2+...+a_n⋅X_n+b $$
Its applications are diverse, spanning fields from finance and medicine to engineering and social science.
For instance, it can be applied to forecast future sales using historical data or explore the interplay between lifestyle choices and health.
While linear regression is a robust and adaptable tool, it's not without limitations. It excels primarily when the variables in question share a linear relationship.
Polynomial Regression
Polynomial regression is a refined regression model where the independent variable x is raised to an nth power. This modification allows the model to fit more intricate data curves.
$$ f(Y)=a_1⋅X_1+a_2⋅X^2_2+...+a_n⋅X^n_n+b $$
Suitable for situations where variables share a curvilinear relationship, this approach offers more flexibility.
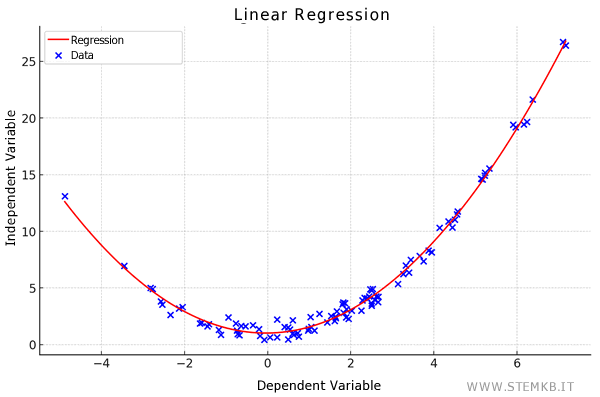
However, polynomial regression can lead to overfitting, especially if the polynomial degree is excessively high, essentially capturing too much noise along with the signal.
Interestingly, polynomial regression is still categorized as a linear model. This might seem paradoxical, but it relates to the model's linear nature in terms of its coefficients (a1,...,an), not the independent variables. In polynomial regression, despite the higher powers of the independent variables creating terms like x2, x3, etc., the relationship between the coefficients and the dependent variable remains linear. In essence, the model still conforms to a linear model framework, wherein each term is linearly multiplied by a coefficient and summed.

