Logistic Regression

Logistic regression, a logit model, plays a pivotal role in machine learning classification algorithms by estimating the likelihood of category membership. This approach is integral to supervised machine learning techniques.

Central to its operation is the logistic function or sigmoid, adept at transforming real-valued inputs into probabilities ranging from 0 to 1.

Note: The term "logistic regression" might suggest a regression algorithm due to its similarity with linear regression. However, it is firmly established as a classification algorithm.

In the training phase, the algorithm is fed a dataset of N examples, each comprising m attributes (X) and a corresponding label (y) for accurate classification.

Training Dataset Example

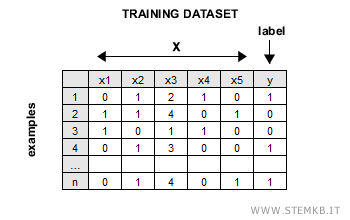
The algorithm seeks an optimal weight vector W that aligns with the attribute vector X_m of each example, aiming to enhance the accuracy of predictions.

The linear combination z of weights W with the attributes X yields the system's response for every training example.

$$ z = W \cdot X = w_1 x_1 + ... + w_m x_m $$

In logistic regression, this linear combination z becomes the argument for the logistic function, which maps it to a probability value between 0 and 1. $$ f(z) = [0,1] $$

This output is then utilized as the activation function in neural network nodes.

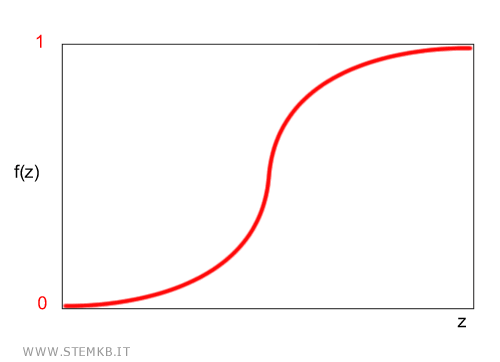
For example, setting a threshold of 0.6 means the node activates when f(z) exceeds 0.6 and remains inactive otherwise.

$$ \begin{cases} 1 \:\: if \:\: f(z)>0.6 \\ \\ 0 \:\: else \end{cases} $$

To identify the most effective weight distribution W*, the algorithm employs a probability maximization function L.

$$ max \: L(W) = \sum_{i=1}^N y_i \log f(z_{(i)}) (x) + (1-y_i) \log (1-f(z_{(i)})) $$

This summation process assesses the model's responses against the correct answers by computing log-probabilities.

Upon completion of training, the algorithm generates a model capable of classifying new examples not included in the initial training set.