Polynomial Identity Examples
The principle of polynomial identity states that two polynomials, P1 and P2, in standard form, are deemed identical if they possess the same degree and identical coefficients for each corresponding variable. This means, for all values of x, P1(x) aligns with P2(x). $$ \forall \ x \ \ \Rightarrow P_1(x) = P_2(x) $$
To illustrate, consider these polynomials:
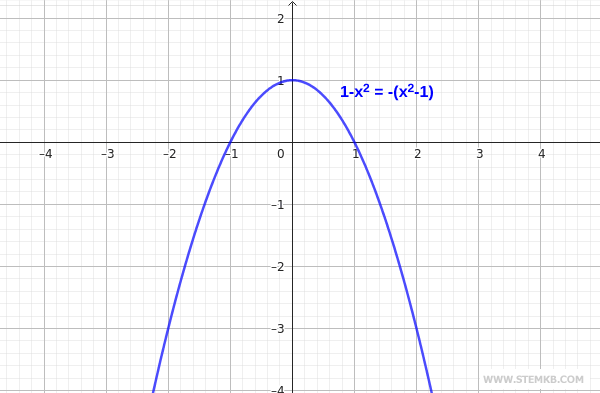
$$ P_1(x) = 1-x^2 $$
$$ P_2(x) = -(x^2-1) $$
As both polynomials are of the same degree, our first criterion is met.
To determine whether the second criterion - matching coefficients - is satisfied, one can manipulate the expressions in such a way that the coefficients of the variables align.
In this case, this task is straightforward. By transforming the second polynomial, we can achieve an equivalent form:
$$ P_1(x) = 1-x^2 $$
$$ P_2(x) = -(x^2-1) = -x^2 +1 = 1-x^2 $$
Hence, both polynomials not only share the same degree (2), but also feature matching coefficients for the x2, x1, and x0 terms, which are 1, 0, and -1, respectively.
$$ P_1 = P_2 $$
Therefore, we can conclude that P1 and P2 are identical polynomials.
Bear in mind that identical polynomials will yield the same output when the same values are substituted for their variables. This results in them having identical graphical representations. The converse is also true: if two polynomials exhibit identical graphs, then they are indeed identical polynomials.