Order of an Element in a Group
The order of an element \( g \) in a group \( (G, \cdot) \), commonly referred to as \( |g| \), is defined as the smallest positive integer \( r \) for which $ g^r $ equals the group's identity element $ e $, succinctly expressed as $$ g^r = e $$
When such a positive integer $ r $ is found, it indicates that the element $ g $ possesses an order of n.
Conversely, if no such integer exists—meaning repeated application of the group operation on \( g \) never yields the identity element—then \( g \) is considered to have an infinite order.
This scenario is typically observed in infinite groups, such as \( (Z, +) \), which denotes the integers under addition.
In a more hands-on approach, for finite groups like \( (Z_n, +) \), an element's order represents how many times the element must be added to itself until the sum is congruent to zero modulo \( n \), aligning with the identity element in modular addition.
Illustrative Examples
To demystify the concept, consider the following examples:
In the group \( (Z_4, +) \), where \( Z_4 \) signifies equivalence classes modulo \( 4 \), the element \( 1 \) boasts an order of \( 4 \) as \( 1+1+1+1 = 4 \equiv 0 \) modulo \( 4 \).
This illustrates that adding \( 1 \) to itself four times effectively results in \( 0 \), the identity element of the group.
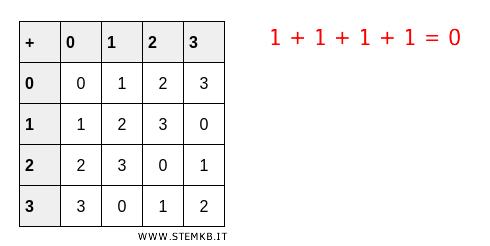
Example 2
Also, in \( (Z_4, +) \), the element \( 2 \) is determined to have an order of \( 2 \) because \( 2+2 = 4 \equiv 0 \) modulo \( 4 \).
This example shows that reaching the identity element requires only two additions.
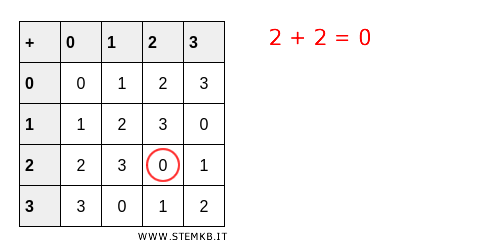
Example 3
Exploring the order of element \( 3 \) in \( Z_4 \) yields:
$$ 3 + 3 \equiv 6 \equiv 2 \mod 4 $$
$$ 3 + 3 + 3 \equiv 9 \equiv 1 \mod 4 $$
$$ 3 + 3 + 3 + 3 \equiv 12 \equiv 0 \mod 4 $$
The journey to 0 modulo 4 is not immediate, as neither the first nor the second addition accomplishes this.
However, the cumulative effect of adding \( 3 \) four times is what achieves a sum of 0 modulo 4, demonstrating that \( 3 \) has an order of 4 in \( Z_4 \) because four is the least positive integer that, when multiplied by \( 3 \), results in a multiple of 4, equivalent to achieving congruency with 0 modulo 4.
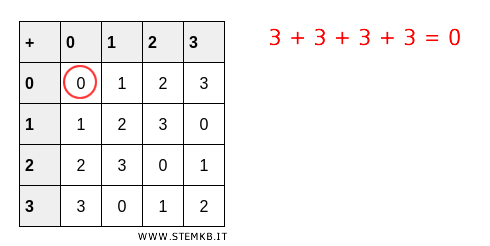
Example 4
The identity element invariably holds an order of \( 1 \), as it inherently satisfies \( e = e \), by definition.
Take, for instance, the group \( (Z_4, +) \) modulo 4, where zero is intrinsically the identity element of the group.
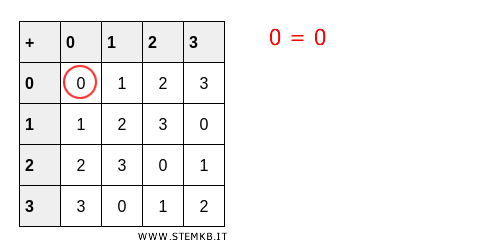
Example 5
In the realm of \( (Z, +) \), representing all integers under addition, any nonzero element \( a \) invariably exhibits an infinite order.
This occurs because starting from any point other than \( 0 \), no amount of self-addition of \( a \) will ever converge on the identity element \( 0 \).
The concept of an element's order within a group plays a pivotal role in abstract algebra and group theory, impacting the structural dynamics of groups and their properties, such as cyclicality or the feasibility of constructing subgroups generated by single elements.
```html
Infinite Order of an Element
When an element \( g \) in a group \( G \) possesses an infinite order, it implies that for any positive integer \( n \), the power \( g^n \) never equals the group's neutral element \( e \), with the sole exception being \( g^0 = e \), which is universally true by definition across all groups.
This means if we select two integers \( s \) and \( t \) where \( s \neq t \), then \( g^s \) and \( g^t \) represent distinct elements within the group \( G \).
The reason behind this is that with \( g \) having an infinite order, no two distinct powers will yield the same result.
Example
Take, for instance, the additive group \( \mathbb{Z} \), which consists of all integers under addition. In this group, \( 0 \) serves as the neutral element, and every integer (every element) has an infinite order: for no integer \( n \), other than zero, does adding \( n \) to itself a finite number of times result in \( 0 \).
If we choose \( g = 1 \) within \( \mathbb{Z} \), it's evident that for any two distinct integers \( s \) and \( t \), \( g^s = s \) and \( g^t = t \) will always be different, given \( s \) and \( t \) are distinct integers.
The cyclic subgroup generated by \( g \), in this case \( \langle g \rangle = \{ ..., -3, -2, -1, 0, 1, 2, 3, ... \} \), is clearly infinite as it encompasses an endless number of elements.
This example demonstrates how an element with an infinite order within a group \( G \) leads to the creation of an infinite cyclic subgroup \( \langle g \rangle \).
Finite Order of an Element
If an element \( g \) in a group \( G \) has a finite period \( n \), then this element \( g \) generates a cyclic subgroup \( \langle g \rangle \) with \( n \) as its total number of distinct elements.
This subgroup is represented as \( \langle g \rangle = \{ e, g, g^2, \ldots, g^{n-1} \} \), where \( e \) is the identity element of the group, also understood as \( g^0 \).
For any pair of integers \( s \) and \( t \), the elements \( g^s \) and \( g^t \) will be the same if and only if \( s \) and \( t \) are congruent modulo \( n \), meaning \( s \) equals \( t \) plus a multiple of \( n \).
Example
Let's consider the group of rotations of a circle, where each rotation is defined by an angle, and the group operation is the composition of rotations.
The group is denoted by \( G \), and the identity element is a 0-degree rotation, representing the identity (no rotation).
Let \( g \) be an element of \( G \) that represents a 60-degree rotation. The period of \( g \) is \( n = 6 \) because after six 60-degree rotations, we return to the initial position: \( g^6 = e \), where \( e \) is the identity element.
The cyclic subgroup generated by \( g \), denoted \( <g> \), consists of all elements that can be represented as powers of \( g \):
$$ <g> = \{ g^0, g^1, g^2, g^3, g^4, g^5 \} $$
Where:
\( g^0 = e \) (the 0-degree rotation)
\( g^1 \) is a 60-degree rotation
\( g^2 \) is a 120-degree rotation
\( g^3 \) is a 180-degree rotation
\( g^4 \) is a 240-degree rotation
\( g^5 \) is a 300-degree rotation
The subgroup \( <g> \) has a cardinality of \( n = 6 \), meaning it contains six distinct elements.
Now, regarding the equality of powers, if we take two integers \( s \) and \( t \) such that \( g^s = g^t \), this will be true if and only if \( s \) is congruent to \( t \) modulo \( n \).
For example, if \( s = 8 \) and \( t = 2 \), we have \( g^8 = g^2 \) because \( 8 \) is congruent to \( 2 \) modulo \( 6 \) (i.e., \( 8 \) differs from \( 2 \) by a multiple of \( 6 \)).
In terms of rotations, this means that a 480-degree rotation (equivalent to \( g^8 \)) brings us to the same position as a 120-degree rotation (equivalent to \( g^2 \)), since both rotations are separated by complete multiples of 360 degrees, corresponding to a full rotation and therefore not altering the final position.

