Scalar Multiplication

In this lesson, we'll delve into the concept of scalar multiplication of a vector, exploring what it entails and the method of calculating it.

Essentially, scalar multiplication of a vector refers to the multiplication of a vector by a constant factor or a real scalar number, symbolized as λ $$ \lambda \cdot \vec{v} $$

Here, lambda can be any real number.

For the purposes of this discussion, let's assign the value of two to lambda.

$$ \lambda = 2 $$

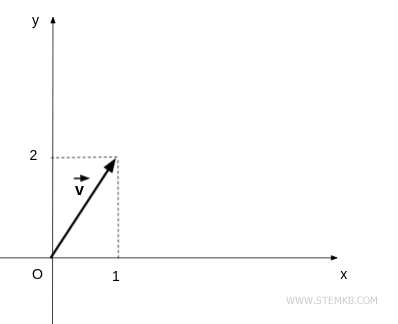
Next, consider a vector with the components x=1 and y=2.

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

This is how it would be represented on a plane.

To perform scalar multiplication, each component of the vector is multiplied by the scalar.

$$ \lambda \cdot \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ \lambda \cdot \vec{v} = \begin{pmatrix} 2 \cdot 1 \\ 2 \cdot 2 \end{pmatrix} $$

What we obtain is the scalar multiplication of the vector when lambda=2.

$$ \lambda \cdot \vec{v} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

The result of scalar multiplication is another vector.

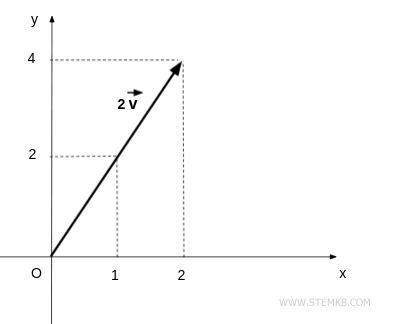
The magnitude or length of the resulting vector is the product of the absolute value of lambda and the magnitude of the original vector.

In this specific case, the length of the resulting vector is twice that of the original vector.

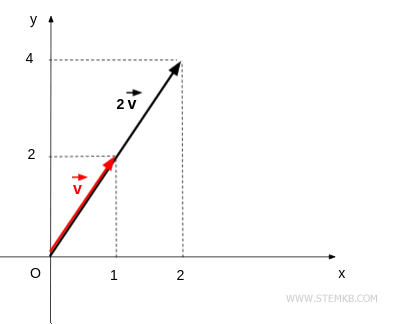
While the direction of the product vector aligns with that of the initial vector, the orientation of the product vector hinges on the sign of the scalar lambda.

• With a positive scalar (λ>0), the orientation remains unchanged.
• Conversely, with a negative scalar (λ<0), the orientation is inverted.

To better illuminate this point, let's examine another example.

Let's multiply the vector by a negative scalar, say lambda = -2.

$$ \lambda \cdot \vec{v} = -2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -2 \cdot 1 \\ -2 \cdot 2 \end{pmatrix} = \begin{pmatrix} -2 \\ -4 \end{pmatrix} $$

The resulting vector possesses twice the magnitude but an inverted orientation relative to the initial vector.

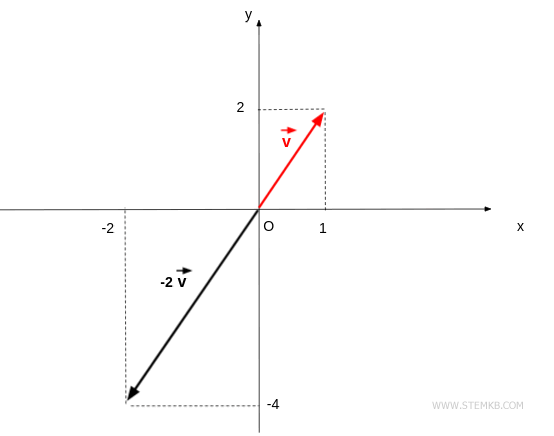
Of note, multiplying the vector by the scalar lambda = -1 yields the opposite vector, i.e., a vector with identical direction and magnitude, but reversed orientation.

Should you find these lessons from Nigiara insightful, do keep an eye out for future updates.