Subtracting Vectors

Let's delve into the simple, yet essential, operation of vector subtraction. You'll find it bears a close resemblance to vector addition.

Here's the heart of it: when subtracting two vectors, your task is to subtract each corresponding component of the vectors.

So, if we have two vectors, v and w, represented as:

$$ \vec{v} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} $$

$$ \vec{w} = \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} $$

The vector resulting from v - w is given by the difference of corresponding components:

$$ \vec{v} - \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} - \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 - w_1 \\ v_2 - w_2 \\ \vdots \\ v_n - w_n \end{pmatrix} $$

For instance, let's consider two vectors: $$ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} $$ $$ \vec{w} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ Here, the difference vector is obtained by subtracting the components of the second vector from those of the first, which leads to: $$ \vec{v} - \vec{w} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 3-1 \\ 4-2 \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$

Another perspective to approach vector subtraction is considering it as adding the first vector, v, to the opposite vector of the second, w.

To illustrate, let's use the same vectors v and w from before:

$$ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} $$ $$ \vec{w} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

In this scenario, the operation of subtracting the second vector from the first is essentially the same as adding the first vector to the opposite of the second, resulting in the following:

$$ \vec{v} - \vec{w} = \vec{v} + ( - \vec{w } ) $$

$$ \vec{v} - \vec{w} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} + ( - \begin{pmatrix} 1 \\ 2 \end{pmatrix} ) $$

$$ \vec{v} - \vec{w} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} + \begin{pmatrix} -1 \\ -2 \end{pmatrix} ) $$

$$ \vec{v} - \vec{w} = \begin{pmatrix} 3-1 \\ 4-2 \end{pmatrix} $$

The final outcome remains the same:

$$ \vec{v} - \vec{w} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$

Geometrically speaking, you can think of vector subtraction as drawing a vector from the tip of the second vector to the first. This vector can then be shifted to start from the origin. This resulting vector represents the difference.

For instance, plot the vectors v=(3;4) and w=(1,2) from the previous example on a plane.

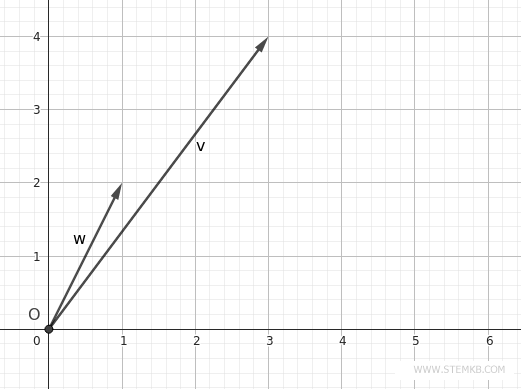
To depict the difference v-w, sketch a vector that joins the tip of the second vector w (the one being subtracted) to the first vector v (the one from which we are subtracting).

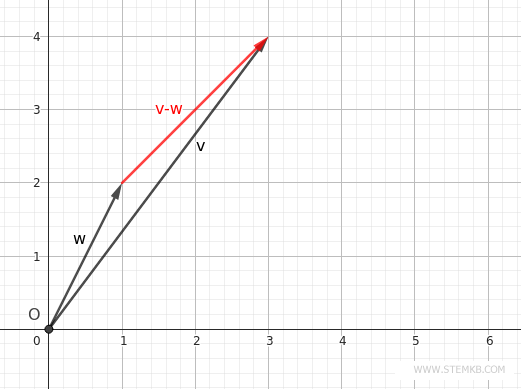
Then shift this vector v-w to start from the origin (O).

The final result is the difference vector.

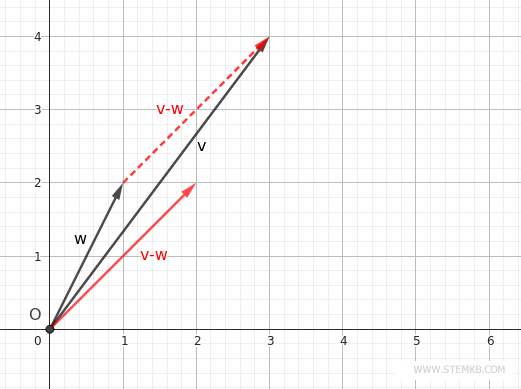
I trust this simplifies the concept of vector subtraction. Don't hesitate to reach out should you have further inquiries regarding vectors.