Complex conjugate in Octave

In this lesson, I will explain how to find the conjugate of a complex number in Octave.

What is the complex conjugate? The conjugate of a complex number z=a+bi is a complex number that has the same real part and the imaginary part changed in sign. For example, the complex number z₁=2+3i has the complex conjugate z₂=2-3i, and vice versa.

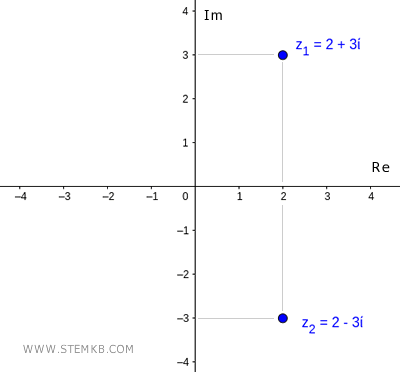
Let me give you a practical example.

Define the complex number z = 2 + 3i in Octave using the function complex(2,3).

>> z=complex(2,3)
ans = 2 + 3i

To obtain the conjugate of a complex number in Octave, you can use the conj() function.

For example, if you have a complex number z=2 + 3i, you can find its conjugate by typing conj(z)

>> conj(z)
ans = 2 - 3i

The function will return the conjugate of the complex number, which in this case is 2 - 3i.

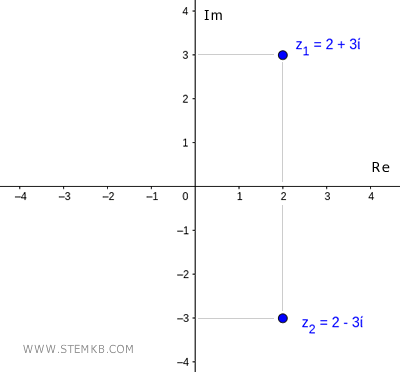
What is the purpose of calculating the complex conjugate?

Calculating the complex conjugate simplifies certain operations in complex number arithmetic.

For example, the product of a complex number with its conjugate is equal to the square of its magnitude.

To calculate, multiply the complex number z by its conjugate conj(z). The product is equal to 13.

>> z*conj(z)
ans = 13

To calculate the modulus of the complex number z, you can use the built-in function abs() in Octave.

The result of applying this function to z is approximately 3.6.

>> abs(z)
ans = 3.6056

Furthermore, calculate the square of the modulus of z.

The result will always be 13.

>> (abs(z))^2
ans = 13.000

This implies that the modulus of a complex number can also be obtained by taking the square root of the product of the complex number and its conjugate.

>> sqrt(z*conj(z))
ans = 3.6056

If you found Nigiara's lesson on using complex numbers in Octave helpful, be sure to keep following us for more.

Nota. In the context of complex numbers, "magnitude" and "modulus" are often used interchangeably to refer to the absolute value or the distance of a complex number from the origin of the complex plane.