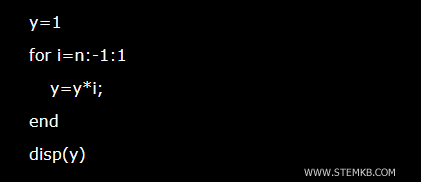Recursive functions in Octave
In this lesson, I will explain how to use recursion in functions on Octave.
Recursion refers to the technique of a function calling itself multiple times. It is a fundamental concept in functional programming.
To help you understand this concept, let me provide you with a practical example.
You can use recursion to calculate the factorial of a number.
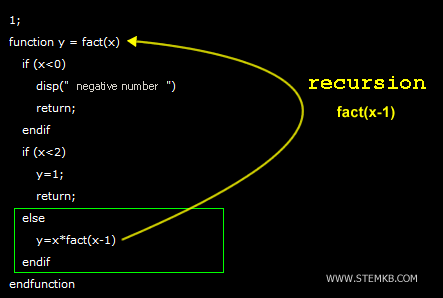
1;
function y = fact(x)
if (x<0)
disp("negative number")
return;
endif
if (x<2)
y=1;
return;
else
y=x*fact(x-1)
endif
endfunction
In this script, I have defined a function called fact() that takes a numerical input (x).
- If x<0
Firstly, the function checks if the input is negative. If x<0, the function displays a message saying that the number is negative and terminates the function call using the return statement. This is because the factorial of a negative number is undefined.

- If 0≤x<2
Next, the function checks if the input is less than 2. If 0≤x<2, the function returns 1 and terminates the recursion. The return statement sends the value 1 back to the previous function call, effectively closing the recursive loop.

- If x≥2
Finally, if the input is greater than or equal to 2, the function multiplies the input number x by the result of fact(x-1). This is achieved through recursion, where the function calls itself with a new input of x-1, which is the current integer number x reduced by one. The process repeats until the base case of x<2 is reached and the recursion terminates.
Overall, this function provides an efficient way of computing factorials of non-negative integers.
For example, you can call the fact() function that you just created and pass 6 as the initial parameter.
The function takes the input number x=6 and recursively calculates the factorial.
n=6
y=fact(n);
disp(y)
The script outputs the number 720, which is the factorial of 6!
720
Why is the output of the function 720?
The function calls itself five times (recursion) by passing a progressively smaller number.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
In the last call fact(1)=1, the function returns 1 because the input value (x=1) is less than two.
At this point, the recursion ends, and the process returns backward by closing all previous calls.
If fact(1)=1 then fact(2)=2 because fact(2)=2*fact(1)=2*1=2
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2
If fact(2)=2 then fact(3)=6 because fact(3)=3*fact(2)=3*2=6
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6
If fact(3)=6 then fact(4)=24 because fact(4)=4*fact(3)=4*6=24
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24
If fact(4)=24 then fact(5)=120 because fact(5)=5*fact(4)=5*24=120
fact(6)=6*fact(5)
fact(5)=5*fact(4)=5*24=120
If fact(5)=120 then fact(6)=720 because fact(6)=6*fact(5)=6*120=720
fact(6)=6*fact(5)=6*120=720
Therefore, the factorial of 6! is 720.
$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$
Note. In this example, I created a factorial function to explain how recursion works in Octave. However, if your need is only to calculate the factorial, remember that Octave also has a specific predefined function, factorial(x), which is much more convenient to use. Additionally, you can calculate the factorial by developing a function based on iteration without using recursion, and the result is always the same.