Finite State Automata

A finite state automaton or finite state machine (FSM) is a mathematical model of a system that can exist in one of a finite number of possible states.

It is particularly useful for representing and managing computational systems with discrete behaviors and a finite number of distinct states, such as communication protocols, digital circuits, and control software.

A finite state automaton consists of five elements:

1. States: A finite set of states, one of which is designated as the initial state. This is generally denoted by the letter $ Q $.
2. Input Alphabet: A finite set of symbols that the automaton can read as input. This is known as the alphabet and is denoted by the uppercase Greek letter $ \Sigma $.
3. Transition Function: A function that maps each pair of a state and an input symbol to a new state. $$ \delta: Q \times \Sigma \rightarrow Q $$ In other words, it indicates the symbols that determine the various actions in each state.
4. Initial State: The state in which the automaton starts. It is an element of the set of states $ q_0 \in Q $.
5. Final States: A subset of states that are considered acceptance or final states. This is denoted by the letter $ F $ and is a subset of the set of states $ F \subseteq Q $.

A finite automaton is formally defined as a 5-tuple, referred to as its formal description.

$$ (Q, \Sigma, \delta, q_0, F ) $$

The finite automaton reads an input string $ w $ from left to right, processing each symbol sequentially and transitioning between states according to the transition function \(\delta\).

Alternatively, the automaton can be depicted using a state diagram.

A change from one state to another is called a transition, which can also be represented using a table known as a transition table.

$$
\begin{array}{c|cc}
 & 0 & 1 \\
\hline
q_0 & q_1 & q_0 \\
q_1 & q_1 & q_2 \\
q_2 & q_1 & q_0 \\
\end{array}
$$

The process begins in the start state \(q_0\) and continues until all symbols of the string have been processed.

If, by the end of the string, the automaton is in an accept state \(F\), the string is accepted; otherwise, it is rejected.

In conclusion, based on the input strings, the automaton's output will be either "accept" or "reject".

Practical Applications. Finite state automata have many applications, including language analysis, pattern recognition, and string validation according to specific syntactic rules. They are also used in the design of digital circuits, such as in discrete control systems (e.g., elevator and traffic light controllers) and in communication protocols to manage the sequence of events in communication networks. They are employed in the lexical analysis phase of compilers for programming languages to recognize tokens in source code.

Finite automata are a key concept in the theory of computation and formal language theory, with applications in many practical areas of computer science and engineering.

Their ability to model sequential behaviors and analyze systems with a finite number of states makes them useful tools for understanding and designing complex systems.

Example of a Finite State Automaton

Consider a deterministic finite automaton \( M \) that recognizes binary strings ending in "01". If the string is recognized, the automaton performs a specific action, such as opening a door. This automaton is defined as follows:

• States: \( Q = \{q_0, q_1, q_2\} \)
• Input Alphabet: \( \Sigma = \{0, 1\} \)
• Transition Function \( \delta \):
  - \(\delta(q_0, 0) = q_1\)
  - \(\delta(q_0, 1) = q_0\)
  - \(\delta(q_1, 0) = q_1\)
  - \(\delta(q_1, 1) = q_2\)
  - \(\delta(q_2, 0) = q_1\)
  - \(\delta(q_2, 1) = q_0\)
• Initial State: \( q_0 \)
• Acceptance State: \( F = \{q_2\} \)

This automaton starts from state \( q_0 \). If it reads "0" when in the initial state, it transitions to \( q_1 \). If it reads "1" in state \( q_1 \), it transitions to \( q_2 \). If it ends in \( q_2 \) after reading the input, the input is accepted.

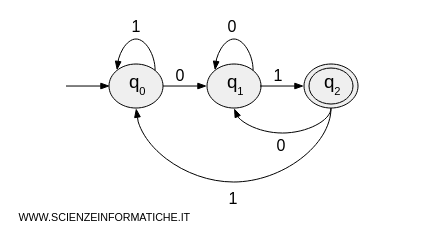
This automaton's operation is graphically represented with this diagram

Typically, acceptance states in the set \( F \) are represented with a double circle, while the initial state is indicated by an arrow pointing to it from nowhere.

In this example, the automaton accepts binary strings that end with "01".

The automaton's transition table is as follows:

$$
\begin{array}{c|cc}
& 0 & 1 \\
\hline
q_0 & q_1 & q_0 \\
q_1 & q_1 & q_2 \\
q_2 & q_1 & q_0 \\
\end{array}
$$

The automaton's response varies based on the input string, leading to either acceptance or rejection of the string.

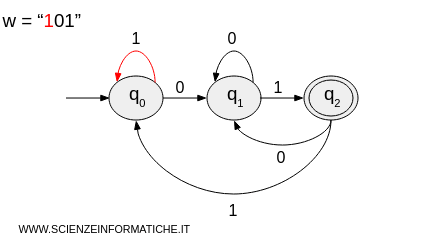
Let's see a practical example with the string w = "101":

1. The machine starts in the initial state \( q_0 \) and processes the first character "1", staying in the same state \( q_0 \).
   
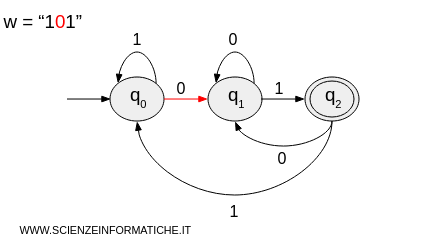
2. It processes the second character "0" and transitions to state \( q_1 \).
   
3. It processes the third and final character "1" and transitions to state \( q_2 \).
   
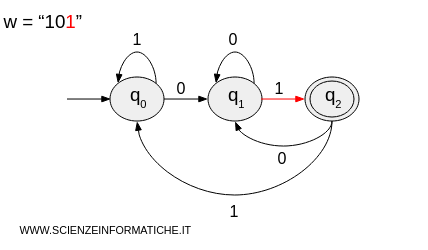
4. The string is finished and the machine is in state \( q_2 \). Since \( q_2 \) is an acceptance state, the machine accepts the string w="101".

Now let's see what happens with the string w = "010":

1. The machine starts in the initial state \( q_0 \) and processes the first character "0", transitioning to state \( q_1 \).
   
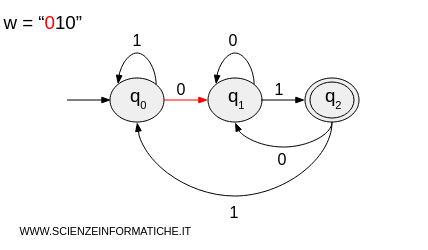
2. It processes the second character "1" and transitions to state \( q_2 \).
   
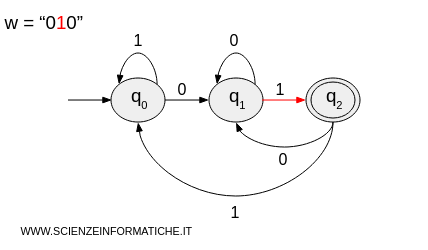
3. It processes the third and final character "0" and transitions to state \( q_1 \).
   
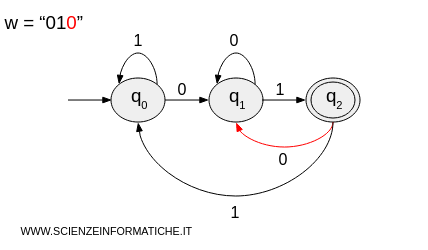
4. The string is finished and the machine is in state \( q_1 \). Since \( q_1 \) is not an acceptance state, the machine rejects the string.

In this example, we analyzed what happens when the machine reads two strings, w="101" and w="010", the machine accepts the first and rejects the second.

The set of all strings accepted by the machine forms a particular set called the language of the machine, \( L(M) \).

The language of the machine is the set of strings accepted by the machine.

Language of the Machine

The language of a finite state machine, denoted as \(L(M)\), is the set of all input strings that the finite automaton \(M\) accepts.

Formally, \(L(M)\) is defined as follows:

\[ L(M) = \{ w \in \Sigma^* \mid M \text{ accepts } w \} \]

Where \(\Sigma^*\) represents the set of all finite strings that can be formed with the alphabet \(\Sigma\).

A string \(w\) is accepted by \(M\) if, starting from the initial state and processing all the symbols of \(w\) according to the transition function \(\delta\), the automaton ends in an acceptance state.

A language is considered a regular language if there exists a finite automaton that can recognize it.

Example of the Machine's Language

Let's consider again the deterministic finite automaton \(M\) that recognizes binary strings ending with "01".

The language \(L(M)\) of the machine \(M\) is the set of all binary strings that end with "01".

Some examples of strings accepted by \(M\) are:

- "01"
- "101"
- "00001"
- "111101"

Formally, we can describe the language \(L(M)\) of this machine as:

\[ L(M) = \{ w \in \{0, 1\}^* \mid w \text{ ends with "01"} \} \]

In other words, \(L(M)\) includes all binary strings that have "01" as their last two symbols.

Any binary string that does not end with "01" will not be accepted by the automaton \(M\).

Types of Finite Automata

There are different types of finite state automata:

• Deterministic Finite Automata (DFA)
  In a DFA, for each state and input symbol, the transition function \(\delta\) specifies exactly one next state. This makes the automaton's behavior completely predictable and deterministic.
• Non-deterministic Finite Automata (NFA)
  In an NFA, the transition function \(\delta\) can specify multiple next states for a given state and input symbol, or even no next state. This introduces a component of non-determinism, where the automaton can follow different execution paths simultaneously.
• Finite Automata with Epsilon Transitions (ε-NFA)
  An ε-NFA is an extension of the NFA that allows "epsilon" transitions, which are transitions that the automaton can make without consuming any input symbols. These transitions provide greater flexibility in defining the automaton's behavior.