Non-deterministic Finite Automata

A Non-deterministic Finite Automaton (NFA) is a computational model where a state and an input symbol can lead to one or more next states, or even to none at all.

In this model, transitions are non-deterministic.

This means that each state can have zero, one, or multiple transitions for the same alphabet symbol, including the epsilon (ε) transition which does not require an input.

Like other automata, an NFA has an initial starting state and one or more final accepting states.

In other words, the transition function maps each state and input symbol pair to a set of states. However, the same symbol in one state might trigger different actions from the automaton, making its behavior unpredictable in advance.

Since a single symbol can cause multiple responses, the NFA must follow every possible state evolution in parallel.

When an NFA reads an input symbol, it can follow multiple paths simultaneously, creating copies of itself.

The NFA accepts a string if at least one of the possible paths ends in an accepting state.

The case of epsilon (ε) transitions. When dealing with a deterministic automaton, ε transitions must also be considered. If a state has an ε transition, the NFA automatically moves to a new state without reading any input symbol.

Formally, a non-deterministic finite automaton is a 5-tuple (Q, Σ, δ, q0, F), where:

  • Q is a finite set of states,
  • Σ is a finite alphabet,
  • δ: Q × Σε → P(Q) is the transition function,
  • q0 ∈ Q is the initial state,
  • F ⊆ Q is the set of accepting states.

Each of these components contributes to the characteristics of the NFA. The best way to understand them is to see them in a practical example.

Practical Example

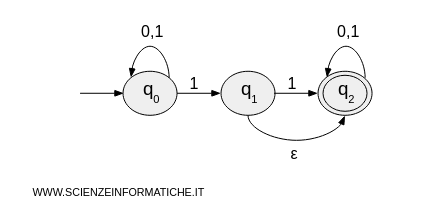
Consider a non-deterministic automaton (Q, Σ, δ, q0, F) that recognizes strings containing the substring '01'.

  • States: \( Q = \{ q_0, q_1, q_2 \} \)
  • Alphabet: \( Σ = \{0, 1 \} \)
  • Transitions (δ)
    - From \( q_0 \) with '0' it stays in \( q_0 \)
    - From \( q_0 \) with '1' it can go to \( q_1 \) or stay in \( q_0 \)
    - From \( q_1 \) with '1' it goes to \( q_2 \)
    - From \( q_1 \) with the empty string 'ε' it goes to \( q_2 \)
    - From \( q_2 \) with '0' or '1' it stays in \( q_2 \)
  • Initial state: \( q_0 \)
  • Accepting states: \( F = \{ q_2 \} \)

The state diagram of the automaton is as follows:

A practical example

Here is the transition table of the automaton:

$$ \begin{array}{c|c|c|c} \ & 0 & 1 & \varepsilon \\ \hline q_0 & \{q_0\} & \{q_0, q_1\} & \emptyset \\ q_1 & \emptyset & \{q_2\} & \{q_2\} \\ q_2 & \{q_2\} & \{q_2\} & \emptyset \\ \end{array} $$

In some states, the transition function has several actions for the same symbol. In other states, there are no available transitions for certain symbols.

Let's see what happens if the automaton reads the string w="010"

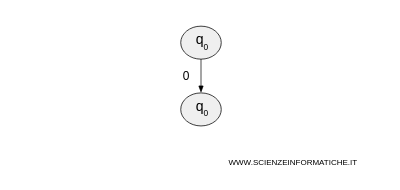
  • The first symbol of the string "010" is 0, and the automaton stays in q0.
    The automaton reads the symbol 0
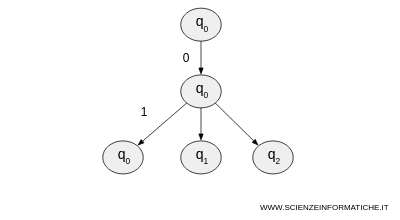
  • The second symbol of the string "010" is 1, and the automaton is in q0. It must follow two paths: stay in q0 or move to q1. Since there is also an ε transition in q1, it must also consider the case where the automaton automatically moves to q2. Therefore, the automaton duplicates itself into three paths and continues to follow them in parallel.
    The automaton reads the symbol 1
  • The third symbol of the string "010" is 0. Let's see what happens in each branch of the computation. In the first branch, the automaton stays in q0. In the second branch, the automaton is in q1 and there are no available transitions with 0, so the string is rejected. In the third branch, the automaton is in q2 and stays in q2.
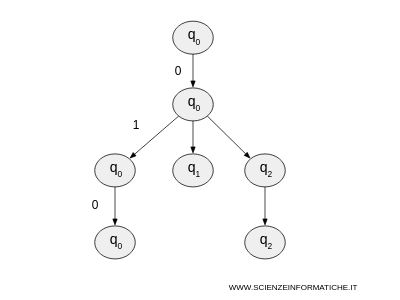
    The automaton reads 0
  • In the third branch, the NFA is in q2, which is an accepting state, so the string "010" is accepted by the automaton.
    The string is accepted by the automaton

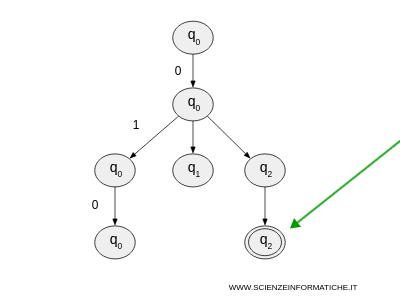
In an NFA, a string is accepted if it is accepted in at least one branch of the computation.

The Difference Between DFA and NFA

The main differences between a Deterministic Finite Automaton (DFA) and a Non-deterministic Finite Automaton (NFA) are as follows:

  • DFA
    In a DFA, each state has exactly one transition for each alphabet symbol. Therefore, the transition function is a single-valued function. Generally, a DFA is simpler to implement but may require more states.
  • NFA
    In an NFA, a state can have multiple transitions for the same symbol or none, and there can be ε transitions. In this case, the transition function is not a single-valued function but rather a relation that maps a state and a symbol to a set of states. An NFA is more compact in terms of states but requires more complex management of transitions because it must follow all possible state evolutions in parallel.

In conclusion, the difference between DFA and NFA mainly lies in how transitions are defined.

DFAs have a simpler and deterministic structure, while NFAs allow greater flexibility with multiple and non-deterministic transitions.

Any NFA can be converted to an equivalent DFA, although the resulting DFA might be larger. Thus, NFAs are a good starting point for understanding and building more complex computational models.

Transforming NFA to DFA

Every non-deterministic finite automaton (NFA) can be transformed into a deterministic finite automaton (DFA).

This means that both NFAs and DFAs accept the same regular language.

Example

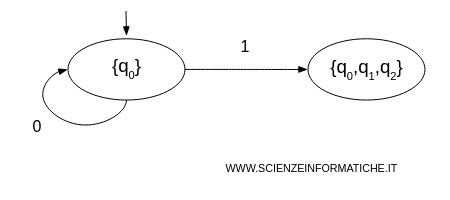
Let's consider this non-deterministic finite automaton (NFA).

A practical example

The automaton has three states {q0,q1,q2}, an entry state q0, and an accepting state q2.

To transform it into a DFA, we proceed with the following steps:

1] The States of the DFA

Given the set of states Q={q0,q1,q2} of the NFA, we determine the power set of Q as the set of states of the DFA.

$$ Q' = \{ \emptyset, \{ q_0 \}, \{ q_1 \}, \{ q_2 \}, \{ q_0, q_1 \}, \{ q_0, q_2 \}, \{ q_1, q_2 \}, \{ q_0, q_1, q_2 \} \} $$

These are all the possible subsets of states that can be reached in the NFA.

2] Initial State of the DFA

We identify the entry state of the DFA by taking the entry states of the NFA obtained before evaluating any symbol, including ε transitions.

In this case, the entry state is the same $ q_0 $.

3] Accepting States of the DFA

The accepting states of the DFA are all subsets of P(Q) that contain the accepting state of the NFA.

In this case, the accepting state of the NFA is q2.

Therefore, the accepting states of the DFA are the subsets containing q2.

$$ F' = \{ \{ q_2 \}, \{ q_0, q_2 \}, \{ q_1, q_2 \}, \{ q_0, q_1, q_2 \} \} $$

4] Transition Function of the DFA

We build the transition function starting from the initial state, evaluating the effects of each alphabet symbol x.

  • State q0
    If x=0, the next transition leads to $$ δ(q_0,0) = \{ q_0 \} $$ If x=1, the automaton stays in q0 or moves to q1 and automatically to q2 via the empty string. Therefore, the automaton moves to the state {q0,q1,q2} of the DFA. $$ δ(q_0,1) = \{ q_0, q_1, q_2 \} $$
    from state q0
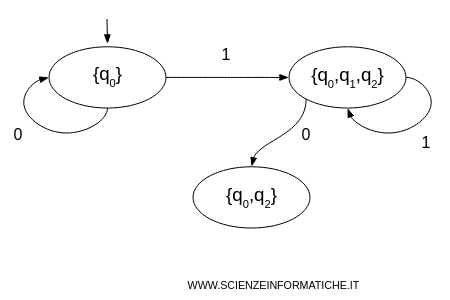
  • State {q0,q1,q2}
    If x=0, the next transition leads to $$ δ(q_0,0) ∪ δ(q_1,0) ∪ δ(q_2,0) = \{q_0\} ∪ \emptyset ∪ \{q_2 \} = \{q_0, q_2 \} $$ If x=1, the next transition leads to $$ δ(q_0,1) ∪ δ(q_1,1) ∪ δ(q_2,1) = \{q_0, q_1, q_2 \} ∪ \{q_2\} ∪ \{q_2 \} = \{q_0, q_1, q_2 \} $$
    from state {q0,q1,q2}
  • State {q0,q2}
    If x=0, the next transition leads to $$ δ(q_0,0) ∪ δ(q_2,0) = \{q_0\} ∪ \{q_2 \} = \{q_0, q_2 \} $$ If x=1, the next transition leads to $$ δ(q_0,1) ∪ δ(q_2,1) = \{q_0, q_1, q_2 \} ∪ \{q_2\} = \{q_0, q_1, q_2 \} $$
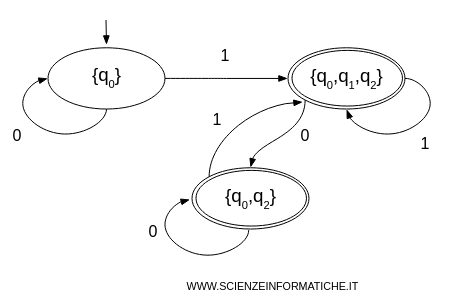
    from state {q0,q2}

The final result is a deterministic finite automaton.

The double circles indicate the accepting states of the DFA, which include the accepting state q2 of the NFA.



Report a mistake or post a question



FacebookTwitterLinkedinLinkedin