
Gradient of a Function
What Exactly Is the Gradient?
The gradient is a vector operator that tells us how a quantity changes across space.
Think of it this way: when you apply the gradient to a scalar function - a function that assigns a single number to every point - you get a vector that points in the direction where the function increases most rapidly. The longer the vector, the faster the increase.
Formally, if you have a scalar function \( f(x, y, z) \) depending on the spatial coordinates \( x \), \( y \), and \( z \), the gradient is calculated as:
\[ \nabla f = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} + \frac{\partial f}{\partial z} \vec{k} \]
where:
- \( \frac{\partial f}{\partial x} \), \( \frac{\partial f}{\partial y} \), and \( \frac{\partial f}{\partial z} \) are the partial derivatives,
- \( \vec{i} \), \( \vec{j} \), and \( \vec{k} \) are the unit vectors along the \( x \)-, \( y \)-, and \( z \)-axes.
If the function only depends on \( x \) and \( y \), the \( z \)-term simply drops out.
Why Does the Gradient Matter?
At a glance, the gradient shows you the fastest way to climb - and how steep the climb is.
As Nobel Prize-winning physicist Richard Feynman put it, "nature always follows the simplest path." In fields like temperature maps, force fields, or mountain landscapes, the gradient is the mathematical tool that reveals that path.
At any point, the gradient gives you two key insights:
- Direction: Where the function increases fastest.
- Magnitude: How steep the increase is.
Imagine standing on a hilltop, wondering where to walk to reach the summit as quickly as possible. That's exactly what the gradient tells you.

Let's See It in Action: The Gradient of a Paraboloid
Take the function:
\[ f(x, y) = x^2 + y^2 \]
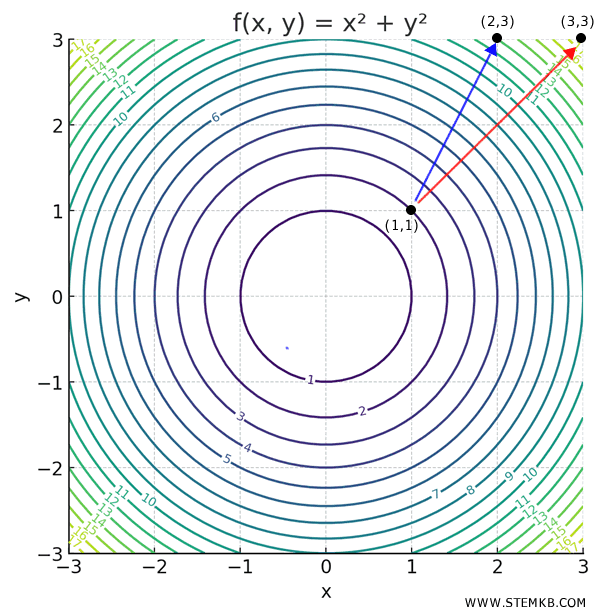
This represents a paraboloid - a surface that gets higher as you move away from the origin.
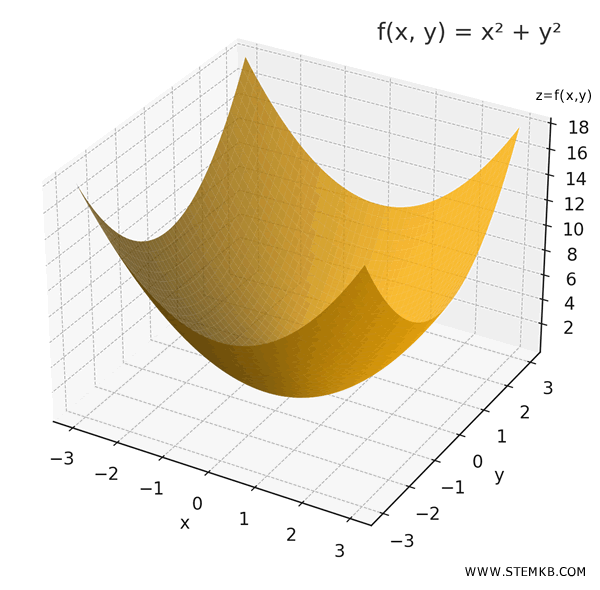
To get a clearer picture, we can also look at its level curves:
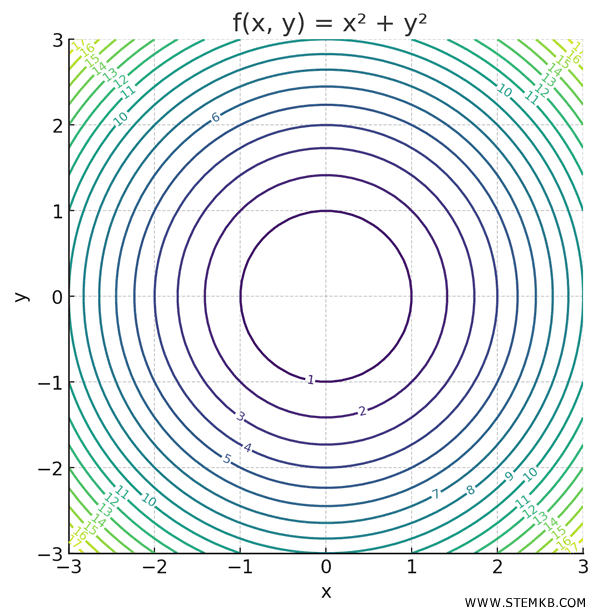
Now, let's find the gradient:
- Differentiate with respect to \( x \): \[ \frac{\partial f}{\partial x} = 2x \]
- Differentiate with respect to \( y \): \[ \frac{\partial f}{\partial y} = 2y \]
Thus, the gradient becomes:
\[ \nabla f = 2x \vec{i} + 2y \vec{j} \]
or simply:
\[ \nabla f = (2x, 2y) \]
What Does This Tell Us?
As you move farther from the origin, the gradient points straight outward - and the farther you go, the steeper the climb.
For instance, at \((1,1)\):
\[ \nabla f(1,1) = (2,2) \]
Meaning, from (1,1), the fastest way up is toward (3,3), at a \( 45^\circ \) angle from the axes.
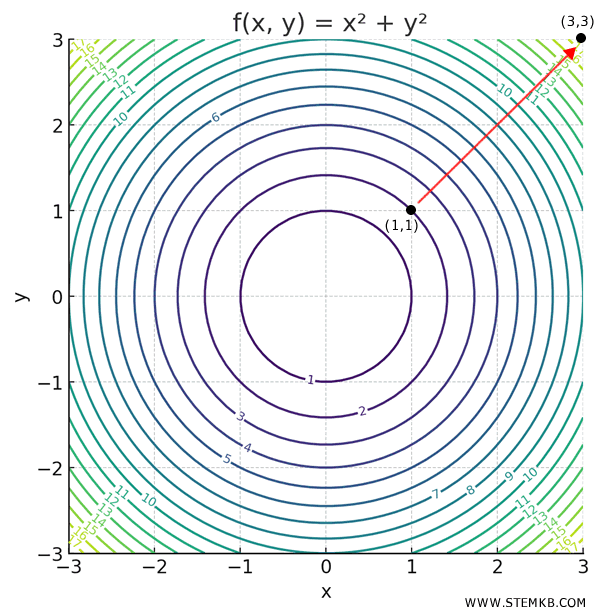
How Steep Is the Climb?
To find out, we calculate the magnitude of the gradient:
\[ \|\nabla f(1,1)\| = \sqrt{(2)^2 + (2)^2} = \sqrt{8} \approx 2.83 \]
In other words, every step you take in the gradient’s direction increases the function’s value by about 2.83 units.
Of course, depending on the function, gradients can behave differently - sometimes even pointing inward. But one rule always holds: the gradient points toward the path of fastest increase. It's like a built-in compass for scalar fields.
What If You Want to Move in a Different Direction?
Sometimes, you're not following the steepest climb - maybe you're sticking to a trail or heading toward a goal.
That’s where the directional derivative comes in. It’s defined as:
\[ D_{\vec{v}} f = \nabla f \cdot \vec{v} \]
Here, \( \vec{v} \) is a unit vector showing the direction you're interested in. The directional derivative tells you how fast the function increases (or decreases) as you move in that specific direction.
Worked Example
Let’s reuse the same function:
\[ f(x, y) = x^2 + y^2 \]
Suppose you want to move from (1,1) toward (2,3), along the vector \( (1,2) \).
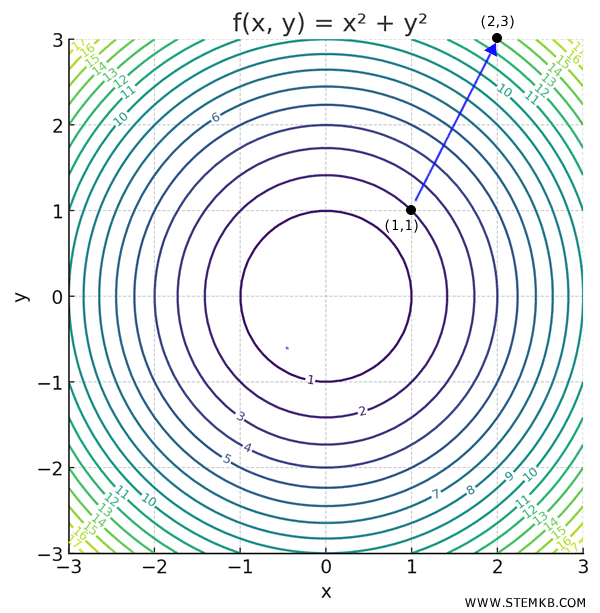
Step 1: Normalize the Direction
First, find the magnitude of the vector:
\[ \|\vec{v}\| = \sqrt{1^2 + 2^2} = \sqrt{5} \]
The unit vector is:
\[ \vec{u} = \left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}}\right) \]
Step 2: Compute the Gradient
We already know the gradient at (1,1):
\[ \nabla f(1,1) = (2,2) \]
Step 3: Calculate the Directional Derivative
Now, take the dot product:
\[ D_{\vec{u}} f(1,1) = (2,2) \cdot \left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}}\right) \]
Which gives:
\[ D_{\vec{u}} f(1,1) = \frac{2}{\sqrt{5}} + \frac{4}{\sqrt{5}} = \frac{6}{\sqrt{5}} \approx 2.68 \]
So, moving from (1,1) in the (1,2) direction, the function increases at a rate of about 2.68 units per unit step.
Notice how 2.68 is slightly less than the maximum rate (2.83) we found earlier. That's because you're not moving in the steepest direction - just a pretty steep one!

