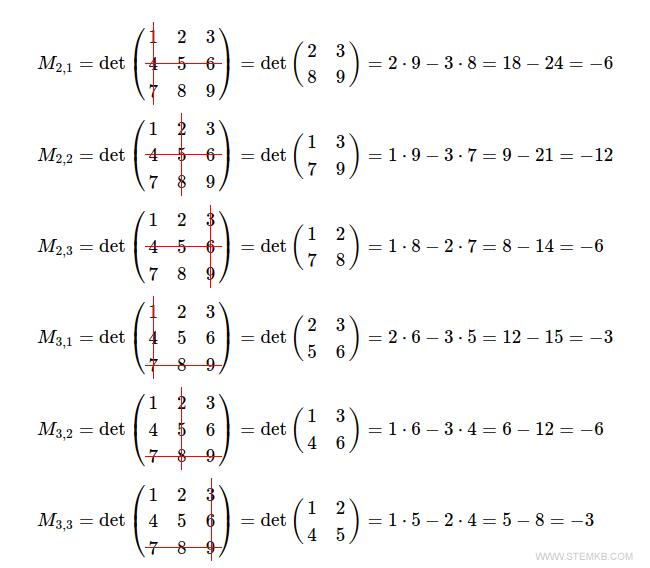Minor of a Matrix
In mathematics, a matrix's "minor" is defined as the determinant of a square submatrix, achieved by eliminating one or more rows and/or columns from the larger matrix.
This process is applicable to both square and rectangular matrices, with the number of minors equating to the quantity of extractable square submatrices.
The relevance of these minors? They play various roles in linear algebra, like calculating the determinant of a 3x3 or 4x4 matrix via Laplace's method or determining the inverse of a matrix.
Let's examine a generic 3x3 matrix.
$$ M = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} $$
Removing the second row and third column, we're left with a square submatrix S2,3
$$ S_{2,3} \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \begin{pmatrix} a & b \\ g & h \end{pmatrix} $$
Thus, the minor M2,3 becomes the determinant of the square submatrix S2,3
$$ M_{2,3} = \det \begin{pmatrix} a & b \\ g & h \end{pmatrix} = a \cdot h - b \cdot g $$
Using this approach, all the matrix's minors can be computed.
However, remember that this is applicable only to square submatrices; rectangular submatrices should be disregarded.
So, how many minors can a 3x3 matrix have?
It adds up to 19 minors, broken down as follows:
- One 3rd-order minor
This is the determinant of the 3x3 matrix itself.
$$ \det M = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} $$ - Nine 2nd-order minors
The determinants of the 2x2 matrices, each formed by removing a row and a column.
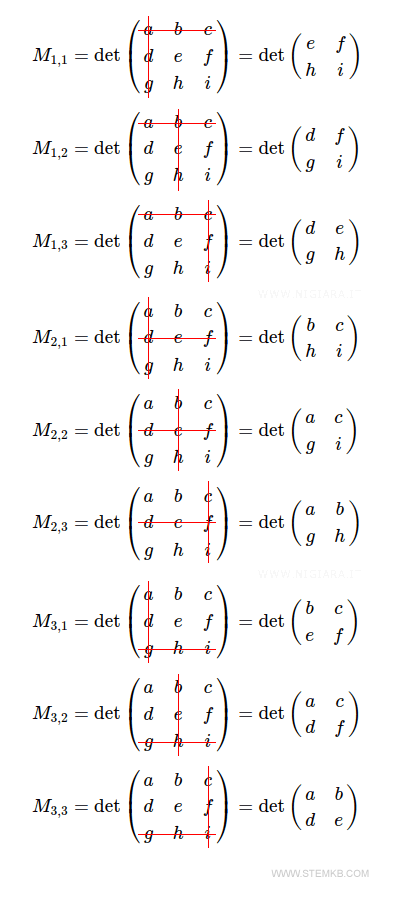
- Nine 1st-order minors
The individual elements of the 3x3 matrix, each formed by removing two rows and two columns. The determinant of a single element equals the value of that element.
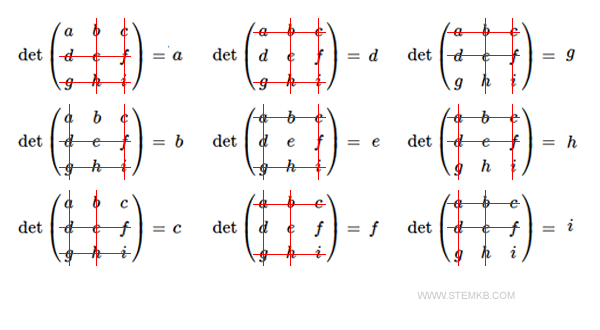
In total, this sums up to 9 + 9 + 1 = 19 minors.
As matrix dimensions increase, so does the complexity of minor calculations. For instance, a 4x4 matrix has a staggering 176 minors, requiring you to calculate the determinant of 16 different 3x3 matrices, the determinant of 144 2x2 matrices, and the determinant of the 16 matrix elements.
To illustrate with a numeric matrix, consider:
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$
Here, the 3rd-order minor of matrix M is the determinant of the matrix itself, which equals zero in this case.
$$ \det M = \det \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$$
$$ \det M = 1 \cdot 5 \cdot 9 + 2 \cdot 6 \cdot 7 + 3 \cdot 4 \cdot 8 - 3 \cdot 5 \cdot 7 - 2 \cdot 4 \cdot 9 - 1 \cdot 6 \cdot 8$$
$$ \det M = 0 $$
The 2nd-order minors are obtained by calculating the determinants of the 2x2 square submatrices.
As an example, minor M1,1 is the determinant of the 2x2 square submatrix that results from eliminating the first row and the first column.
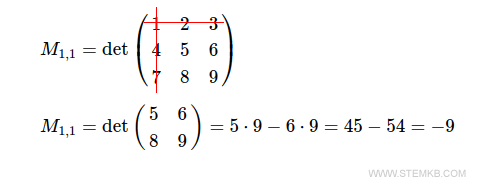
The minor M1,2 is the determinant of the 2x2 square submatrix that you get by eliminating the first row and the second column.
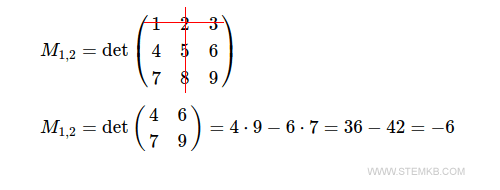
The minor M1,3 is the determinant of the 2x2 square submatrix that you get by eliminating the first row and the third column.
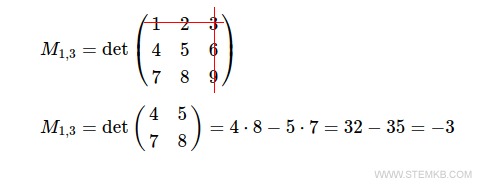
By following the same procedure, you can calculate the remaining 2nd-order minors of matrix M.