Matrix Multiplication

The process of multiplying matrices requires the utilization of the row-by-column method.

Let's delve into an illustrative example using two 2x2 square matrices, denoted here as A and B.

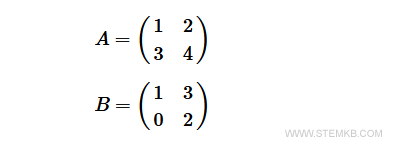
Initiate by multiplying the first row of matrix A by the first column of matrix B.

The result of this computation is then positioned in the first row and first column of the resultant matrix AB.

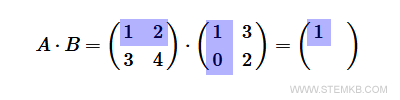
It's simple. The first element (1) of the first row in A is multiplied by the first element (1) of the first column in B. Subsequently, the second element (2) of the first row of A is multiplied with the second element (0) of the first column of B. Sum these products to obtain: $$ 1 \cdot 1 + 2 \cdot 0 = 1 + 0 = 1 $$ The resultant figure is then placed in the first row and column of the product matrix AB. This operation is referred to as the linear combination of two vectors.

Continue by multiplying the first row of matrix A by the second column of matrix B.

The outcome should be recorded in the first row and second column of the matrix AB.

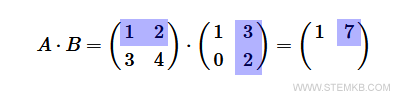
The detailed calculation follows: $$ 1 \cdot 3 + 2 \cdot 2 = 3 + 4 = 7 $$

Next, perform a multiplication of the second row of matrix A and the first column of matrix B.

Place the result in the second row and first column of the product matrix AB.

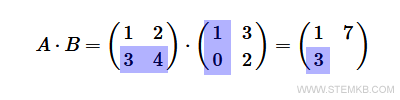
Here's the in-depth computation: $$ 3 \cdot 1 + 4 \cdot 0 = 3 + 0 = 3 $$

Lastly, multiply the second row of matrix A by the second column of matrix B.

This result is then written in the second row and second column of the product matrix AB.

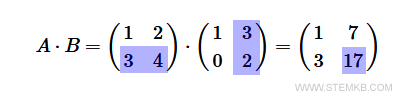
To break down the calculation: $$ 3 \cdot 3 + 4 \cdot 2 = 9 + 8 = 17 $$

Now you've successfully derived the product matrix.

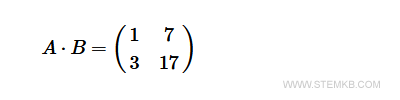
It's crucial to remember that the multiplication of two matrices can only be performed if the number of columns in the first matrix aligns with the number of rows in the second matrix.

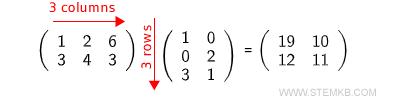
Lastly, bear in mind that unlike certain mathematical operations, matrix multiplication does not possess the commutative property.

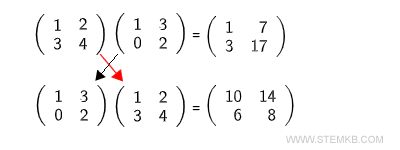
In conclusion, understanding the row-by-column product method is a vital component in linear algebra, as it paves the way for more complex operations and mathematical explorations.