How to do the inverse matrix in Geogebra

In this lesson I'll explain how to calculate the inverse matrix using Geogebra.

What is an inverse matrix? A matrix A is invertible if there is an inverse matrix B, such that the vector product AxB returns an identity matrix.

Create an invertible square matrix.

For example, create a 3x3 matrix with three rows and three columns.

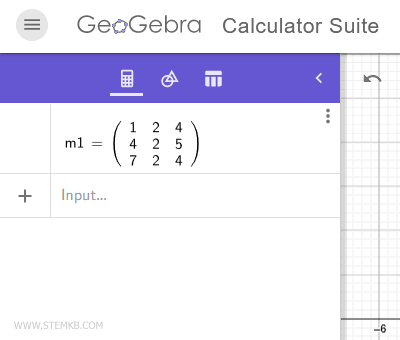
write a square matrix with 3 rows and 3 columns

Note. If you don't know how to do this, read our previous lesson: how to make a matrix in Geogebra.

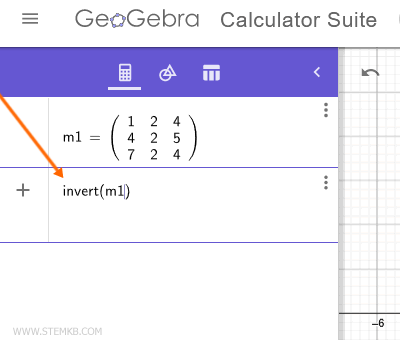
Now type the invert() function in a new Geogebra field.

Write the name of the matrix you just created between the round brackets.

Geogebra calculates and displays the inverse matrix.

the computation of the inverse matrix

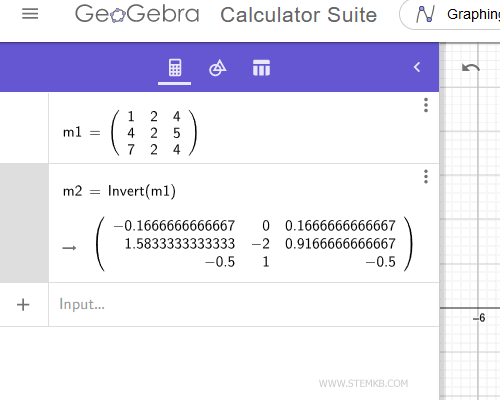
You have calculated the inverse matrix

To do a quick check, multiply the first matrix (invertible) and the second matrix (inverse).

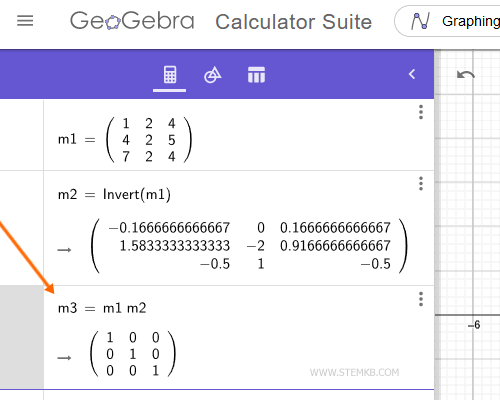
the verification of the inverse matrix

The result of the vector product is an identity matrix. It is a matrix with the elements equal to 1 in the main diagonal and all the other null elements.

If this lesson from StemKB is useful, keep following us.