Categories

A category comprises two fundamental elements: objects and morphisms, or arrows, which connect these objects.

This concept is pivotal in mathematics, particularly within category theory.

Each category includes two essential components:

• Objects: These can vary widely, depending on the category. For instance, they could be sets, spaces, or groups.
• Morphisms: Morphisms serve as the "arrows" linking one object to another. Each has a source and a target object and can be regarded as functions or transformations between objects.

In addition, a category must adhere to these properties:

• Identity: There must be an identity morphism \( id_X \) for each object \( X \) within the category that maps \( X \) to itself. This morphism functions as a neutral element in composition operations, ensuring that for any morphism \( f : X \to Y \), \( f \circ id_X = f \) and \( id_Y \circ f = f \) hold true.
• Composition: Morphisms must adhere to a composition law. If \( f \) connects \( X \) to \( Y \), and \( g \) connects \( Y \) to \( Z \), then a morphism \( g \circ f \) should exist that connects \( X \) to \( Z \). This operation must be associative, implying that for a morphism \( h \) from \( Z \) to another object \( W \), \( h \circ (g \circ f) = (h \circ g) \circ f \) must apply.

Despite its abstract nature, category theory offers a profound lens for exploring and understanding various areas of mathematics and the broader field of science.

A key strength of categories lies in their abstract nature. Starting with tangible concepts like sets and functions, category theory elevates our understanding to a level where we can discuss objects and morphisms in a manner detached from underlying specifics. This abstraction not only simplifies complex issues but also facilitates the exchange of insights and findings across different scientific fields, extending beyond just mathematics.

Example

A straightforward example of a category is the category of sets, often denoted as Set.

The object set in the category Set consists of three sets:

$$ Obj(Set) = \{A, B, C \} $$

Consider three finite sets:

$$ A = \{1, 2, 3\} $$

$$ B = \{x, y\} $$

$$ C = \{true, false\} $$

The set of morphisms in the category Set includes two functions:

$$ Mor(Set) = \{ f, g \} $$

As we conclude this discussion, note that the set $ Mor(Set) $ must also account for the compositions of morphisms and the identity morphisms, in addition to these direct morphisms.

Let's examine the functions:

$$ f : A \to B $$

$$ f(1) = x \\ f(2) = x \\ f(3) = y $$

$$ g : B \to C $$

$$ g(x) = true \\ g(y) = false $$

For clarity, let's depict the objects and morphisms within the category using Euler-Venn diagrams:

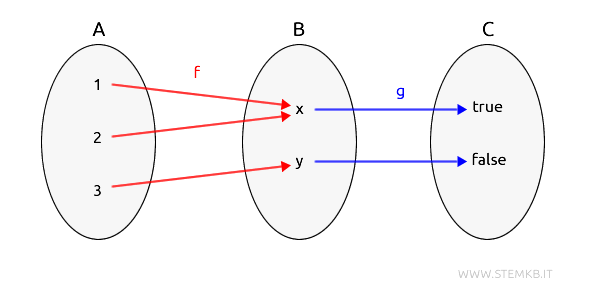
When we compose the two morphisms $ f $ and $ g $, we introduce a composition of morphisms $ g \circ f $ from A to C.

$$ g \circ f : A \to C $$

$$ ( g \circ f)(1) = g(f(1)) = g(x) = true \\ (g \circ f)(2) = g(f(2)) = g(x) = true \\ (g \circ f)(3) = g(f(3)) = g(y) = false $$

In addition, the category includes identity morphisms that connect each object to itself.

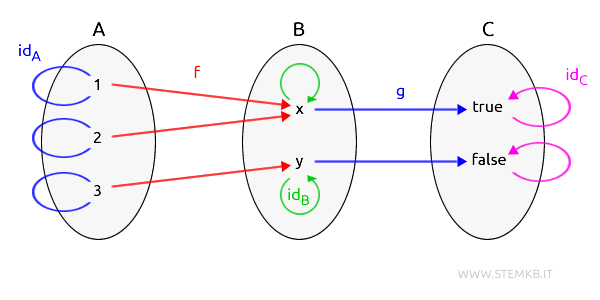
With three objects (sets A, B, C) in this category, there are correspondingly three identity morphisms.

$$ id(A): A \to A $$

$$ id(B): B \to B $$

$$ id(C): B \to C $$

The complete set of morphisms therefore includes the direct morphisms, possible compositions, and identity morphisms.

$$ Mor(Set) = \{ f, g, f \circ g, id(A), id(B), id(C) \} $$

This example clearly demonstrates the dynamic interplay between functions (morphisms) and

Types of Categories: Small and Large

In category theory, we classify categories as either "small" or "large," depending on the scale of their object and morphism sets.

• Small Category
  A small category is defined by having both its object set, Obj(), and its morphism set, Mor(), as actual sets. This implies that both objects and morphisms can be collected into a set that complies with the traditional rules of set theory.

  Typical examples of small categories are the category of finite sets (FinSet) and the category of finite groups (Grp), including their homomorphisms. These are termed "small" because they contain a finite number of objects and morphisms that can be completely described as sets.

• Large Category
  A large category occurs when either the object set or the morphism set constitutes a proper class instead of a set. This suggests that the volume of objects or morphisms exceeds the normal limits of set theory, typical of categories that encompass, for example, all possible sets or all topological spaces.

  The category of all sets (Set), with functions as morphisms, is considered a large category because it includes an ensemble that transcends the confines of a standard set and avoids pitfalls like Russell’s paradox.

The distinction between small and large categories is pivotal because large categories introduce significant challenges in mathematical and logical operations. The techniques employed to handle proper classes are considerably more complex and often necessitate special measures, such as employing universes in certain category theory methodologies.