Morphisms in Category Theory
In category theory, a morphism serves as a function that connects an object A (the domain) to another object B (the codomain) within the same category. $$ f: A \rightarrow B $$ Also referred to as an arrow or map, it's commonly represented as $ f_{AB} $.
Morphisms are essentially functions that establish links between objects in a category. These objects can be any type of mathematical construct, including sets, vector spaces, and groups.
In a category, morphisms are fundamental in defining both the structure of and the relationships among objects. They encapsulate processes, functions, and transformations in a manner consistent with the category's mathematical framework.
Each morphism is characterized by a starting point (domain) and an endpoint (codomain), which may or may not be the same.
$$ f: \underbrace{A}_{\text{domain}} \rightarrow \underbrace{B}_{\text{codomain}} $$
Moreover, morphisms have a specific directionality. As such, the morphisms $ f_{AB} $ and $ f_{BA} $ represent distinct pathways between the same pair of objects.
Properties of Morphisms
Morphisms adhere to three fundamental properties:
- Start and End Points
Every morphism functions as an arrow that originates from a "domain" and targets a "codomain." Therefore, a morphism inherently has a start and an end. $$ f: \underbrace{A}_{\text{dom(f)}} \rightarrow \underbrace{B}_{\text{cod(f)}} $$ - Composition of Morphisms
If you have two morphisms, $ f \in hom(A,B) $ and $ g \in hom(B,C) $, where the codomain of the first is the domain of the second, you can compose them to forge a new morphism. $$ f ∘ g \in hom(A,C) $$
If a morphism exists from A to B (f: A → B) and another from B to C (g: B → C), there must also be a morphism from A to C (g ∘ f: A → C), resulting from the composition of f and g. This composition adheres to the associative property, which ensures that the grouping of morphisms during composition does not alter the outcome. $$ f ∘ (g∘h) = (f∘g)∘h $$
- Identity Morphisms
Each object features an identity morphism that effectively "points" back to itself $ 1A \in hom(A,A) $. This identity morphism acts as a neutral element in compositions, ensuring that any composition with other applicable morphisms yields the original morphism.
For every object A, there is an identity morphism (1A: A → A) that acts as the neutral element in compositions. Thus, composing an identity morphism with any other morphism leaves the latter unchanged.
Morphisms serve as the structural "glue" of categories, facilitating interactions (through composition) and relationships (through domains and codomains) that define the mathematical properties integral to a category.
The set of all morphisms between two particular objects A and B in the same category is known as hom-sets and is denoted hom(A,B).
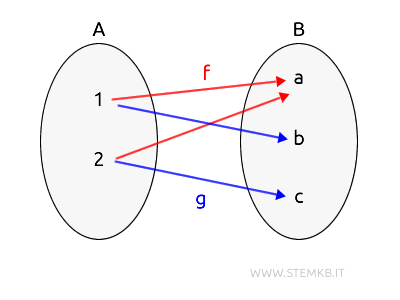
Note that hom(A,B) encompasses all morphisms between the specific objects A and B of the category, particularly those from A to B, and should not be confused with the overall set of morphisms in the category.
The set of all morphisms in a category is another collection ( or class) and is designated by Mor(C), where C denotes the category under discussion.
Example
Consider a simple category known as "Set," where objects are sets and the morphisms are functions between these sets.
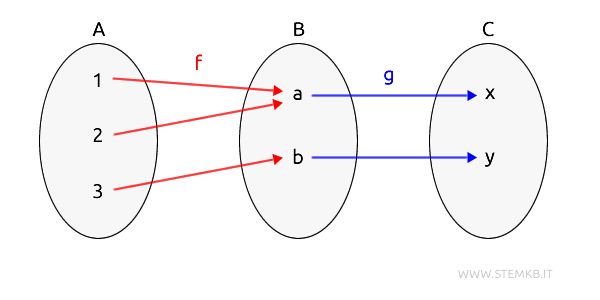
This category features three objects and two directional morphisms.
- Objects
Let A = {1,2,3}, B = {a,b} and C = {x,y} represent three objects of the Set category. $$ Obj(Set) = \{ A,B,C \} $$ where Set is the category. - Morphisms between objects
There are two morphisms (functions) in the category: $$ mor(Set) = \{f,g \} $$- The function \( f: A \rightarrow B \) is defined as follows:
\( f(1) = a \)
\( f(2) = a \)
\( f(3) = b \)
This function \( f \) qualifies as a morphism from object A to object B in the Set category, as it maps each element of A to an element in B. - The function $ g: B \rightarrow C $ operates as follows:
\( g(a) = x \)
\( g(b) = y \)
This function $ g $ also acts as a morphism, linking object B to object C within the Set category.
- The function \( f: A \rightarrow B \) is defined as follows:
- Composition of Morphisms
This example presents a single composition possibility: combining \( f \) and \( g \) results in a morphism \( g \circ f: A \rightarrow C \):
\( g(f(1)) = g(a) = x \)
\( g(f(2)) = g(a) = x \)
\( g(f(3)) = g(b) = y \) - Identity Morphisms
Every set includes an identity morphism. For set A, it's \( 1_A: A \rightarrow A \), mapping each element back to itself. The same holds true for B with \( 1_B: B \rightarrow B \) and C with \( 1_C: C \rightarrow C \).
In this category, functions between sets function as morphisms, and the familiar mathematical rules of composition and identity are clearly reflected.
The set of all morphisms for a specific pair of sets, like A to B, is termed a hom-set and is labeled hom(A, B).
$$ hom(A,B) = \{ f \} $$
$$ hom(B,C) = \{ g \} $$
$$ \hom(A,C) = \{ g \circ f \} $$
Conversely, the set of all morphisms Mor(Set) comprises all possible functions between any pair of sets in the category, including identities and any potential compositions of morphisms.
$$ Mor(Set) = \{ f, g, g \circ f, 1_A, 1_B, 1_C \} $$
This practical illustration clearly demonstrates the operation of morphisms and provides a comprehensive view of the key characteristics of morphisms within a category.

