Identity Morphism in Category Theory

In category theory, the identity morphism for an object $A$ maps every element of \(A\) to itself. This is denoted by $\text{id}_A$ or $1_A$. $$ \forall \ a \ \in A \ , \  \text{id}_A(a) = a $$

Each object \(A\) in a category has an associated identity morphism \( \text{id}_A : A \to A \), which fulfills the following properties:

1. Identity
   On \(A\), the identity morphism \( \text{id}_A \) ensures that each element maps to itself.
2. Morphism Composition
   For any morphisms \(f: A \to B\) and \(g: B \to A\), the composition of \(f\) with \( \text{id}_A \) and \( \text{id}_B \) with \(f\) consistently results in \(f\), demonstrating: $$ f \circ \text{id}_A = f $$ $$ \text{id}_B \circ f = f $$ This highlights how \( \text{id}_A \) and \( \text{id}_B \) serve as neutral elements in morphism composition.

Thus, the identity morphism is crucial in maintaining object integrity within the category, ensuring that morphism composition is coherent and that the category remains operationally closed.

Example

Let's explore a concrete example of a category and its identity morphism to understand its functionality.

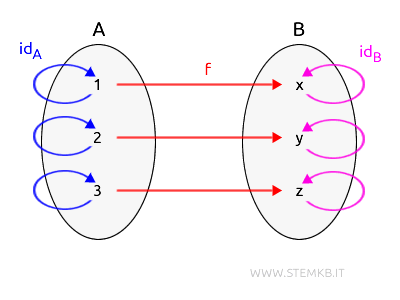
Consider the category called Set, which includes two objects and a morphism:

$$ Obj(Set) = \{ A, B \} $$

Here, A and B are two finite sets:

$$ A = \{1, 2, 3\} $$

$$ B = \{x, y, z\} $$

The category includes a single morphism, f:

$$ Mor(Set) = \{ f , g \} $$

The function \(f: A \rightarrow B\) is defined as:

$$ f(1) = x $$

$$ f(2) = y $$

$$ f(3) = z $$

By definition, each object in Set is equipped with an identity morphism that maps every element to itself:

The identity morphisms for $A$ and $B$ are:

$$ \text{id}_A: A \rightarrow A $$

$$ \text{id}_B: B \rightarrow B $$

Now, if we consider the composition of \(f\) with \( \text{id}_A \):

$$ f \circ \text{id}_A: A \rightarrow B $$

This operation first applies \( \text{id}_A \) and then \(f\).

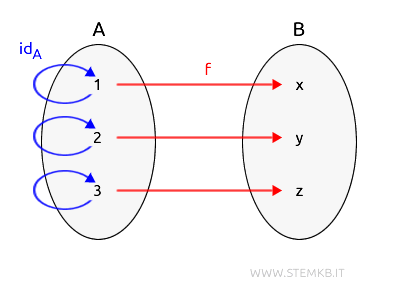
Since \( \text{id}_A \) leaves the elements of \(A\) unchanged, \( f \circ \text{id}_A \) is effectively identical to \(f\):

$$ f \circ \text{id}_A(1) = f(1) = x $$

$$ f \circ \text{id}_A(2) = f(2) = y $$

$$ f \circ \text{id}_A(3) = f(3) = z $$

In a similar vein, the composition of \( \text{id}_B \) with \( f \) yields:

$$ \text{id}_B \circ f: A \rightarrow B $$

This sequence involves applying \(f\) followed by \( \text{id}_B \).

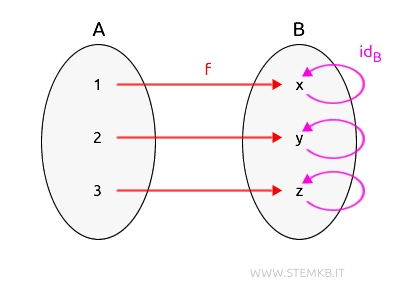
Since \( \text{id}_B \) does not alter the elements of \(B\), \( \text{id}_B \circ f \) remains true to \(f\):

$$ \text{id}_B \circ f(1) = \text{id}_B(x) = x $$

$$ \text{id}_B \circ f(2) = \text{id}_B(y) = y $$

$$ \text{id}_B \circ f(3) = \text{id}_B(z) = z $$

This example vividly demonstrates how identity morphisms preserve the functional dynamics