Set Union

Suppose we have two sets, A and B, and we want to bring them together. This union forms a new set that encapsulates all elements from A and B. In mathematical parlance, we denote this as $$ A \cup B $$

Let's delve into a practical example to illuminate this concept further.

Assume we have two finite sets:

$$ A = \{ 1, 2, 3 \} $$

$$ B = \{ 2, 3, 4, 5 \} $$

Set A comprises three distinct elements, namely {1, 2, 3}, whereas set B consists of four unique elements {2, 3, 4, 5}.

When we speak of the union of two sets, A and B, we are referring to a set that embodies all elements found in either set A or B, or even in both.

This can be depicted as:

$$ A \cup B = \{ 1, 2, 3 \} \cup \{ 2, 3, 4 \} $$

which simplifies to:

$$ A \cup B = \{ 1, 2, 3, 4, 5 \} $$

Thus, our resultant union set consists of five elements: A ∪ B={1,2,3,4,5}.

Another way to grasp this concept is through the lens of Euler-Venn diagrams.

Picture the two sets, their individual areas, and imagine how they would overlap. The union is the total area of these two intersecting sets.

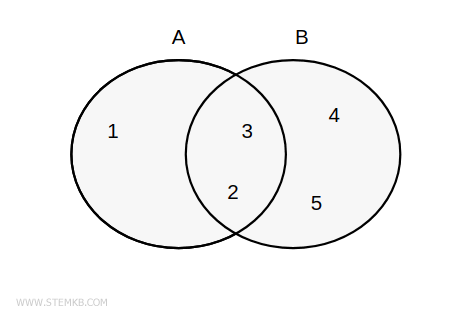
It's crucial to note that there might be elements that appear in both sets. In our example, these are the elements 2 and 3. Yet, when forming the union set, we count these elements just once. Why is this? Well, one fundamental rule of sets is that they cannot contain identical elements more than once. It's part of what makes a set a set.