Sets Intersection

In this tutorial we delve into the concept of intersection within the realm of set theory, providing tangible examples along the way.

To put it simply, the intersection of two sets, A and B, results in a new set that comprises elements common to both A and B. In set notation, the intersection of two sets is denoted by the symbol ∩. In other words, $$ A \cap B $$

So, if we have two sets, A and B, their intersection gives us a set comprising only those elements present in both A and B.

The process to ascertain this intersection involves comparing elements of the two sets and identifying those shared by both.

From a geometric perspective, the intersection of two sets represents the area where the sets overlap. Now, let's examine this concept with some real-world examples.

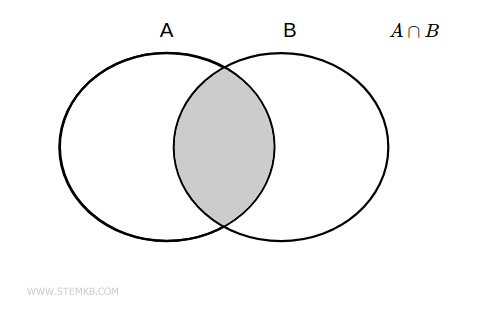
Take for instance, two sets A and B.

$$ A = \{1, 2, 3, 4 \} $$

$$ B = \{3, 4, 5, 6 \} $$

Each set contains certain integers.

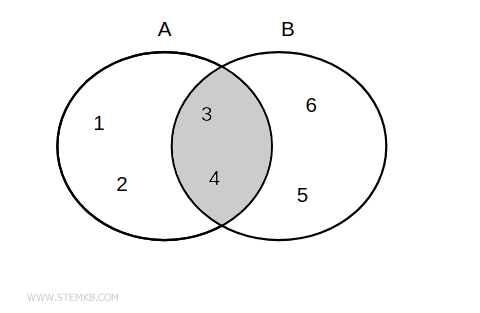
The intersection of these two sets, achieved by identifying elements common to both A and B, results in the set {3, 4}, since these numbers are found in both sets.

$$ A \cap B = \{ 3, 4 \} $$

But why is understanding intersections important? Well, they can be quite useful in a number of scenarios. If you're working with data, intersections can help identify commonalities between two datasets, facilitating effective comparison. Moreover, intersections come in handy while solving mathematical problems, such as finding the points where two mathematical functions intersect.

Now, let's take a look at another practical application of intersections:

Example 1

Let's assume you have two sets of even numbers:

$$ A = \{2, 4, 6, 8, 10 \} $$

$$ B = \{4, 8, 12, 16 \} $$

Here, the intersection A∩B results in the set {4, 8}, as these are the only elements common to both sets.

$$ A \cap B = \{4, 8 \} $$

For simpler or smaller sets, you could use Euler-Venn diagrams to visually represent the sets and their intersection.

Example 2

For a less numerical example, consider two sets A and B containing city names:

$$ A = \{\text{Milan, Rome, Florence, Naples} \} $$

$$ B = \{\text{Venice, Rome, Naple, Bologna} \} $$

The intersection of these two sets is {Rome, Naples}, as these cities appear in both sets.

$$ A \cap B = \{\text{Rome, Naple} \} $$