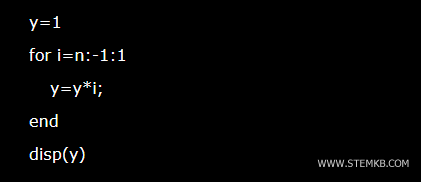Recursive Functions in Matlab
I was just thinking about this topic of recursive functions in Matlab, and I figured I'd share a few thoughts on it.
What is recursion? A recursive function is a function that calls itself one or more times. This technique is a fundamental concept in functional programming, and it can be really useful in solving certain types of problems.
Let me give you an example.
Suppose you want to calculate the factorial of a number (n!). You could define a recursive function like this:
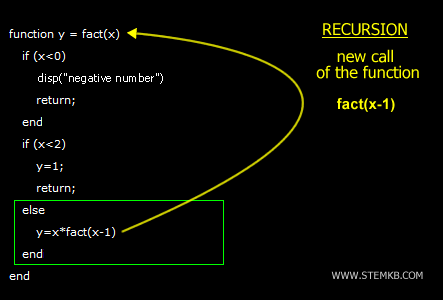
function y = fact(x)
if (x<0)
disp("negative number")
return;
end
if (x<2)
y=1;
return;
else
y=x*fact(x-1);
end
end
This function, fact(), is a recursive function because it calls itself in the statement y = x * fact(x - 1).
Now, let me walk you through how it works.
First, the function fact() receives a number x as input through the call.
- If x<0
If x is negative, the function does nothing because the factorial of a negative number does not exist. In this case, the function prints "negative number" and returns control to the calling program through the return statement.

- If 0≤x<2
If x is a positive number less than 2, the function returns 1. In this case, the recursion terminates because the function does not call itself. The return statement returns the value 1 to the previous recursive call of the function, and the process goes back, closing the previous recursive calls.

- If x≥2
If x is greater than or equal to 2, the function multiplies the number x by the result of the function fact(x - 1). In this case, the function calls itself fact(x - 1) recursively.
For example, let's call the function fact() with the number x = 6.
n=6;
y=fact(n);
disp(y)
function y = fact(x)
if (x<0)
disp("negative number")
return;
end
if (x<2)
y=1;
return;
else
y=x*fact(x-1);
end
end
Note. Remember that a function in Matlab must always be defined at the end of the script.
The function receives the input number x = 6 and starts to calculate the factorial 6! recursively.
The function calls itself 5 times (recursion), passing each time a number lower than the previous one.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
In the last call fact(1) = 1, the function returns 1, closing the previous recursive calls.
If fact(1) = 1, then fact(2) = 2 because fact(2) = 2 * fact(1) = 2 * 1 = 2.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2
If fact(2) = 2, then fact(3) = 6 because fact(3) = 3 * fact(2) = 3 * 2 = 6.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6
If fact(3) = 6, then fact(4) must be equal to 24. Why, you ask? It's simple, really. You just take fact(4) and multiply it by 4, which gives you 4 times fact(3), which we know is 6, so that comes out to be 24.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24
We know that fact(5) is equal to 5 times fact(4), which we just determined is 24. So, fact(5) must be 120.
fact(6)=6*fact(5)
fact(5)=5*fact(4)=5*24=120
And if fact(5) is 120, then fact(6) must be 6 times 120, which is 720.
fact(6)=6*fact(5)=6*120=720
So, there you have it!
$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$
The factorial of 6 is 720.
720
Note. Note that in this example, we have created a recursive function to calculate the factorial of a number. This is a useful example to explain how recursion works. However, you can also use the pre-defined factorial(x) function in Matlab to calculate the factorial without defining another function.
factorial(6)=720
You can also calculate the factorial of a number by developing an iterative function without using recursion. In either case, the final result is always the same.
Here is an example algorithm for calculating the factorial using iteration: