Scilab's uint8() Function

In Scilab, the utility of the uint8() function is undeniable. This function facilitates the conversion of numbers into an 8-bit unsigned integer format.

uint8(x)

Here, 'x' represents either a single number or an array of numbers you wish to convert.

The function subsequently returns the number as an 8-bit unsigned integer.

For those less familiar, the term "uint8" denotes an 8-bit unsigned integer. This integer lies within a range from 0 to 255. It's crucial to understand that a single bit possesses only two potential values: 0 or 1. Thus, the apex of an integer value that can be represented using 8 bits is 255. In binary notation, this is presented as 11111111, tantamount to 1 byte.

Implementing the uint8() function within Scilab is refreshingly simple.

Consider a floating-point number:

x=221.9

To transform this number into its 8-bit unsigned integer equivalent, you'd deploy the uint8(x) function.

uint8(x)

Promptly, the function renders the integer value of 221.

221

However, it's noteworthy that if your numerical input exceeds the maximal 8-bit unsigned integer boundary of 255, Scilab recalibrates by commencing its count anew. This behavior can be attributed to the principles of modular arithmetic for integers.

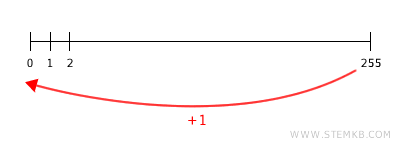
For example, adding one to 255 yields 0:

uint(255+1)

0

Incrementing 255 by two results in 1:

uint(255+1)

1

Conversely, values falling beneath the minimum (0) prompt Scilab to count backward from the peak value.

As an illustration, deducting one from zero yields 255:

uint(0-1)

255

It's salient to recognize that in these scenarios, Scilab doesn’t produce an overflow error. Instead, it leans on the tenets of modular arithmetic.

So, what's the ideal scenario for deploying the uint8() function? It emerges as a potent tool when there's a need to store positive integer data that spans between 0 and 255 without consuming excessive memory. Take the RGB systems, for instance. Here, the color values of images are demarcated by three integers, each oscillating between 0 and 255. These integers typify the intensity levels of the red, green, and blue hues. Resorting to integers that span 16 bits or more for this task would be an unwarranted expenditure of memory resources.