The int16() Function in Scilab

In the world of Scilab, the int16() function stands out as a crucial tool. Its primary role? To seamlessly convert numbers, or even entire matrices of numbers, into a 16-bit signed integer format. Here's the basic syntax:

int16(x)

Here, 'x' can be either a singular decimal number or an entire matrix of them.

Depending on your input, the function will gracefully return a 16-bit integer for individual numbers or a corresponding set of 16-bit integers for matrices.

Now, you might wonder: what exactly is a 16-bit integer? It's a specialized numeric data type occupying a modest 16 bits of memory. Considering that each bit represents a binary choice of 0 or 1, this format can account for a sum of 2^16, which equals 65,536 distinct numbers. To put it simply, it can depict numbers from -32,768 all the way up to 32,767.

Let's illustrate its use with a basic example.

Suppose you craft a matrix of decimal numbers like so:

M = [1.2, 2.7; 3.5, 4.9];

To convert this matrix using int16()

int16(M)

The output? An integer matrix.

ans =
1 2
3 4

But here's an interesting quandary: what if the number overshoots 32,767?

In such scenarios, int16() demonstrates its sophistication by employing modular arithmetic, wrapping the number back to -32,768, the lowest in the 16-bit range.

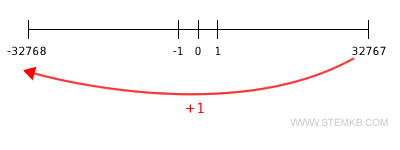
For a clearer picture, in a 16-bit setting, adding 1 to 32,767 yields -32,768:

int16(32767+1)

ans=
-32768

Similarly, adding 2 offers -32767

int16(32767+2)

ans=
-32767

Conversely, if you dip below -32,768, Scilab adjusts by shifting to the range's pinnacle, 32,767.

int16(-32768-1)

ans=
32767

One of the shining attributes of Scilab in these operations is its resilience. Instead of buckling under the pressure of overflow errors, it leans on the robustness of modular arithmetic.

So, why lean on int16()? It's about efficiency. If you're certain that your data snugly fits within the 16-bit integer boundaries, or if you're transitioning data to 16-bit reliant devices, it's invaluable.

But a word to the wise: every conversion from decimal to integer trims the edges, sacrificing a touch of precision.

In conclusion, the int16() function is a potent tool, but like all tools, it's essential to understand its strengths and potential pitfalls.