How to Calculate Absolute Value on Octave

In this lesson I'll explain how to calculate the absolute value of a real number on Octave.

What is absolute value? In mathematics, the absolute value (or modulus) of a real number is a function that transforms a number into a positive number. It is indicated with two vertical bars. $$ |-2| = 2 $$ For example, the absolute value of -2 is 2. Thus, the result is a number that has the same digits but always a positive sign.

I'll give you a practical example

Define a variable with a negative value, for example x=-2

>> x=-2

To calculate the absolute value use the abs(x) function

>> abs(x)
ans = 2

The abs() function returns the absolute value of x.

In this case the result is 2.

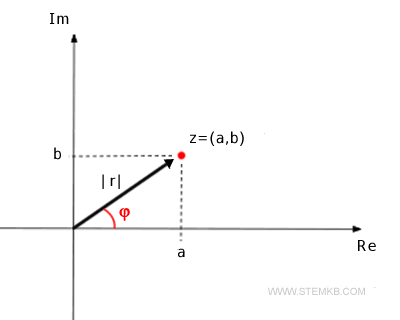
Note. You can also use the abs() function by indicating a complex number as an argument. In this case the function has a different task because it returns the modulus of the complex number. It's the length |r| of the vector joining the origin with the coordinates of the complex number z=(a,b)=a+bi on the Cartesian plane.