How to create a matrix in Octave

In this lesson I teach you how to create a square or rectangular matrix in Octave.

I'll give you a practical example.

This is a simple 2x2 square matrix. The matrix has two rows and two columns.

$$ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

To define this array in Octave you have to use an array variable.

>> m = [ 1 2 ; 3 4 ]

Write all elements of the array in square brackets.

• Separate the elements of a row from each other with a space or a comma.
• Separate the rows from each other with a semicolon.

The result is a 2x2 square matrix.

m =
1 2
3 4

After creating the matrix in Octave, you can use it in any matrix calculation operation.

Example. You can calculate the sum or product of two matrices, the determinant, the rank, the inverse or transpose matrix, etc. For example to calculate the determinant of the matrix use the function det(m).

How to make a rectangular matrix

The procedure for creating a rectangular matrix is the same as you have already seen for creating square matrices.

For example, this is a 3x4 rectangular matrix

$$ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{pmatrix} $$

In this case the matrix has three rows and four columns.

Write the 12 elements of the array in square brackets and separate the elements from each other with a space.

Then add a semicolon to the end of each row of the matrix, except the last row.

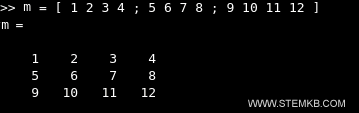
>> m = [ 1 2 3 4 ; 5 6 7 8 ; 9 10 11 12 ]

The result is a rectangular matrix

This way you can create any square or rectangular matrix with any number of rows and columns.

You just have to remember to write the elements starting from the first element to the last and separate the rows with a semicolon.

Note. You can separate items on the same row with a space or a comma. It's the same. Personally I recommend that you separate them with a space because it makes the code more readable. It allows you to better see the semicolons that separate rows.