Creating a Vector in Octave

In this lesson I'll explain how to define vectors in Octave with a practical example.

For example, the vector v(2; 4) has two dimensions

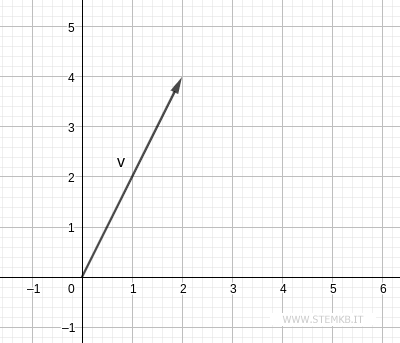
vector example in 2D

The vector has two components x = 2 and y = 4.

To define this vector in Octave use an array variable, separating the components of the vector with semicolons.

>> v=[2;4]

This creates a column vector

$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

After creating the vector you can use it in any vector calculation operation (sum, vector product, scalar product, etc.)

How to create a vector in three dimensional space

Similarly, you can create a vector with three or more components.

For example, the vector v(2;4;3).

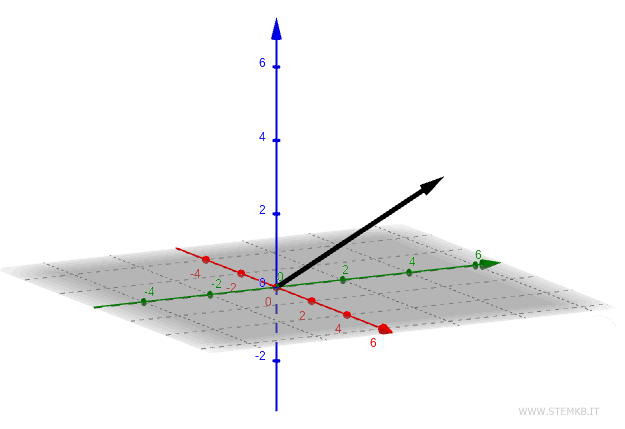
example of 3D vector

This vector has three components x = 2, y = 4, z = 3

$$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix} $$

To define this vector in Octave type

>> v=[2;4;3]

How to create a row vector

In the previous examples I have explained to you how to define a column vector in Octave.

$$ \vec{v} = \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$

However, sometimes it happens that you have to work with a row vector. It is a vector with the elements arranged horizontally.

$$ \vec{v} = \begin{pmatrix} a & b & c \end{pmatrix} $$

To create a row vector in Octave, you just need to separate the components with a space or a comma.

For example, to define this row vector

$$ \vec{v} = \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} $$

Write an array and separate elements with commas

>> v=[1, 2, 3]

The result is a row vector.

Note. There is also another way to create a row vector. Once you have created a column vector, you can transform it into a row vector by transposing it.