The Tangent Function in Scilab

Scilab is equipped with an extensive range of trigonometric functions, one of which is the tangent, represented by the tan() function.

tan(x)

This function requires an angle, expressed in radians, and returns its tangent value.

You have the flexibility to input either a singular value or an array.

When an array is provided, the `tan()` function diligently calculates the tangent for each of its elements. The resulting output is a new array, mirroring the original in terms of element count. It's crucial to note that the tangent's domain is between -π/2 and π/2 radians, equivalent to an interval of -90° to 90°. Additionally, the tangent exhibits periodic behavior, repeating at consistent intervals.

For clarity, consider this example.

To determine the tangent of π/4 radians (45°)

tan(%pi/4)

In Scilab, %pi denotes the mathematical constant pi (π≈3.14).

For π/4 radians, the tangent value is

1.0000000

For those working with degrees, the tangent can still be computed.

However, a conversion from degrees to radians is necessary, achieved using the formula.

$$ \text{radianti} = \text{gradi} \cdot \frac{\pi}{180} $$

For instance, the tangent of 45° can be found with tan(45*%pi/180).

tan(45*%pi/180)

The tangent of a 45° angle is 1.

1.0000000

Moreover, Scilab allows for the computation of the tangent across an array of values, be it a vector or matrix.

To illustrate, let's define a vector "v" with values:

 

v=[0, %pi/6, %pi/4]

Computing the tangent for each array element is as simple as:

 

tan(v)

The output array contains the tangent values corresponding to each element of "v", maintaining the original array's size.

In this instance, we have three elements:

 

0. 0.5773503 1.

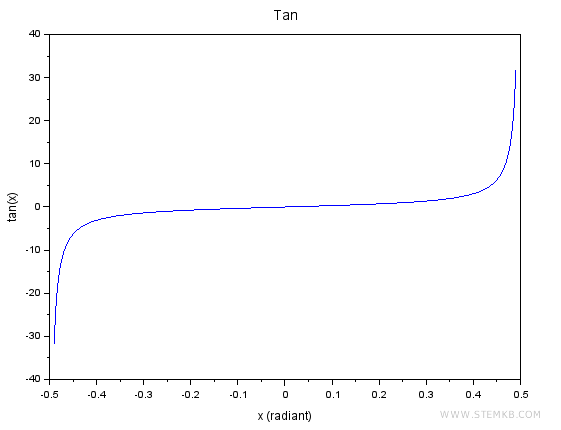
To visualize the tangent function, the following script plots its graph with angles in radians.

clf
x = linspace(-0.49, 0.49, 1000);
y = tan(x * %pi);
xlabel('x (radiant)');
ylabel('tan(x)');
title('Tan');
plot(x, y);

This graphical representation showcases the tangent function between -π/2 and π/2.