How to Create a Vector Field in GeoGebra

In this tutorial, we’ll walk through the steps to create a vector field in GeoGebra. The commands will be in English, so if you’re using GeoGebra in another language, you’ll need to find the equivalent functions in your language.

What is a vector field? A vector field assigns a vector to every point in a given space, representing a quantity with direction and magnitude that can vary across the space. Vector fields are commonly used to model physical phenomena such as fluid flow, electric fields, or magnetic fields. Mathematically, a vector field is defined by a function that outputs a vector for each point in the space.

Let’s see how to create one in GeoGebra.

Open GeoGebra Classic or GeoGebra 3D, depending on your preference. For a two-dimensional vector field, ensure you’re in the 2D Graphics View. For a three-dimensional field, switch to the 3D Graphics View.

Start by defining the function that describes your vector field.

Here’s an example of a rotational field:

$$ \mathbf{F}(x, y) = \begin{bmatrix} y \\ -x \end{bmatrix} $$

To define this in GeoGebra, enter the following commands:

f1(x, y) = y

Followed by:

f2(x, y) = -x

Next, use the `Sequence` command to create the grid of points where the vectors will be displayed:

Sequence[Sequence[(a, b), b, -5, 5, 1], a, -5, 5, 1]

This generates a grid of points ranging from \((-5, -5)\) to \((5, 5)\) with a step size of 1.

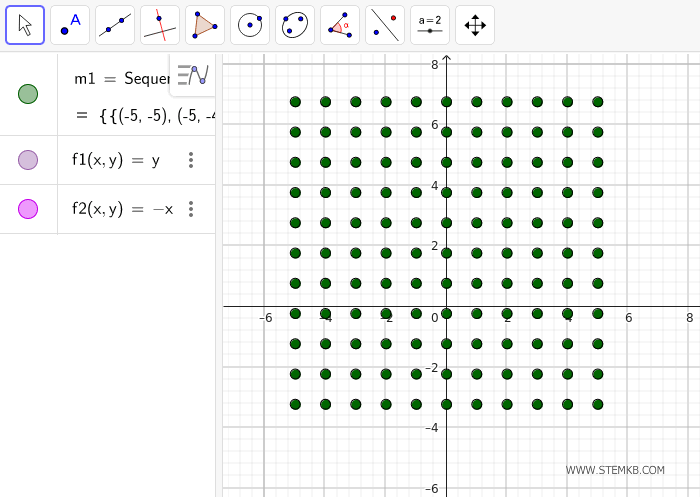
Now, use the `Vector` command to draw vectors at each point based on the defined functions:

Sequence[Sequence[Vector[(a, b), (a + f1(a, b), b + f2(a, b))], b, -5, 5, 1], a, -5, 5, 1]

Here, (a, b) represents the starting point of the vector, while (a + f1(a, b), b + f2(a, b)) specifies the endpoint.

This command creates a vector field over the grid spanning from (−5,−5) to (5,5) with a step size of 1.

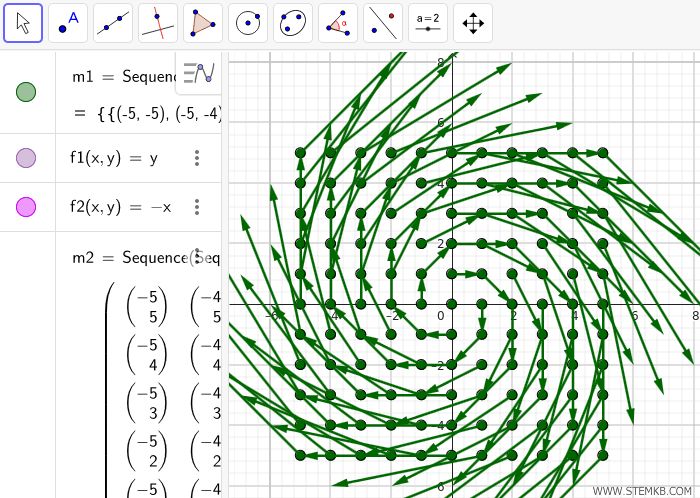
You can now customize the appearance of your vector field.

For instance, you can adjust the style, color, and thickness of the vectors using the properties panel, add labels for better clarity, export the graph as an image, or use sliders to dynamically modify the vector field.

If you want to highlight the vectors, you can hide the origin points for a cleaner visualization.

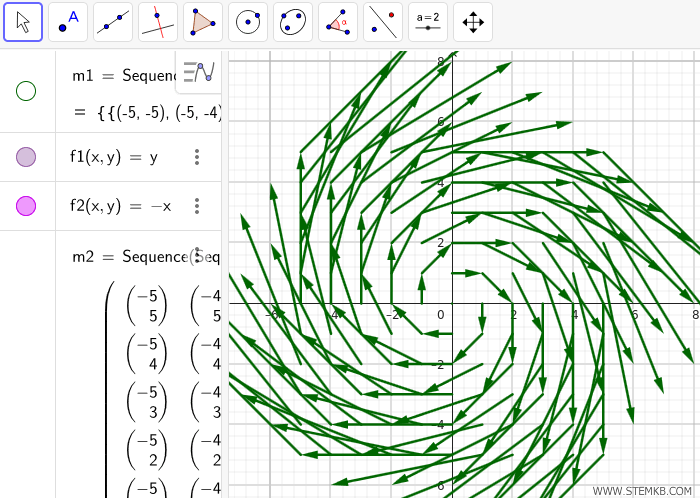
If you’re working with 3D vector fields, the process is similar, but you’ll need to define vectors in three dimensions and use the 3D Graphics View to visualize them.

Don’t forget to save your GeoGebra file if you want to reuse it later!