Norm (Magnitude) of a Vector in GeoGebra

If you're learning about vectors and want to visualize their magnitude, GeoGebra is a powerful tool that makes it easy. In this guide, you’ll learn how to calculate the norm - or length - of a vector using both 2D and 3D views in GeoGebra.

Why does the norm matter? The norm of a vector tells you how long the vector is - essentially, it’s the distance from the origin to the vector’s endpoint. This value is useful for comparing vectors, normalizing them (turning them into unit vectors), and calculating angles between vectors using the dot product.

You can work in either 2D or 3D space - GeoGebra supports both. Let’s start with a simple 2D example.

Working with a 2D vector

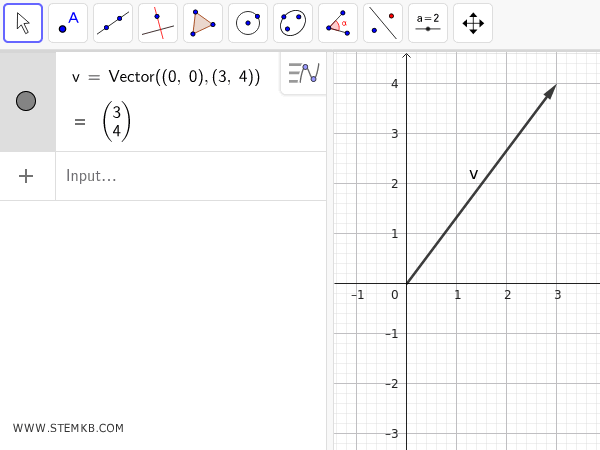
Imagine you want to find the magnitude of this vector:

\[ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} \]

If you're not sure how to input a vector in GeoGebra, check out the lesson on Cartesian vectors. Otherwise, type this directly into the input bar:

v = Vector((0, 0), (3, 4))

This command creates a vector from the origin to the point (3, 4).

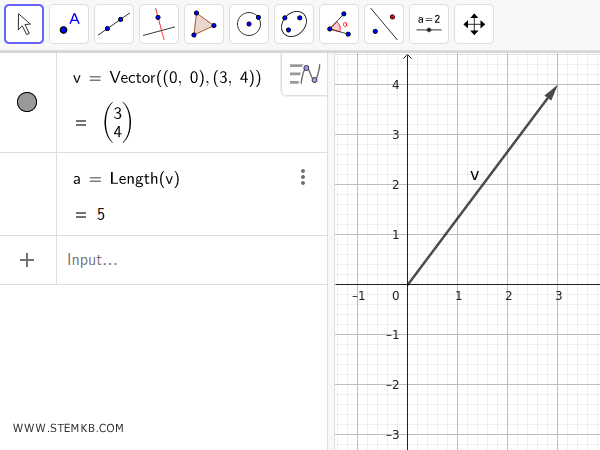
Now, to find the magnitude (or norm) of the vector, just use the Length() function:

Length(v)

GeoGebra will return:

5

That’s the length of the vector - also the distance from its tip to the origin.

Want to double-check? Here’s the math:

\[ \|\vec{v}\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]

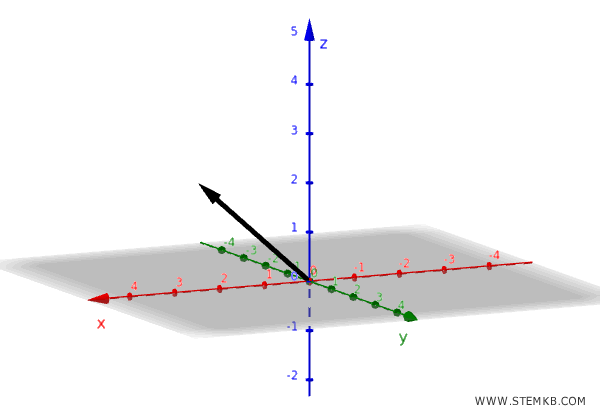
Working with a 3D vector

GeoGebra also supports vectors in 3D. Let’s try this one:

\[ \vec{u} = \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix} \]

Type the following:

u = (2, -1, 2)

Then use Length()

Length(u)

GeoGebra will return:

3

This is the 3D version of vector length. The result is the same as you'd get using the formula:

\[ \|\vec{u}\| = \sqrt{2^2 + (-1)^2 + 2^2} = \sqrt{4 + 1 + 4} = \sqrt{9} = 3 \]

Can you find the norm of a 4D vector?

Not directly. GeoGebra doesn’t support vectors with more than three components as geometric objects. That means you can’t define or graph a 4D vector using Vector() or similar commands.

However, you can still calculate the norm manually using the CAS or Algebra view. For example:

sqrt(1^2 + 2^2 + 3^2 + 4^2)

Or using a list:

v := {1, 2, 3, 4}
sqrt(Sum(v^2))

In this case, GeoGebra works like a symbolic calculator. You won’t get a graphical representation, but you can still compute the result accurately.

If you found this quick guide from StemKB helpful, stick around for more tips on using GeoGebra and exploring math visually!