
Absolute Value of an Integer
The absolute value (also known as the modulus) of an integer \( a \), written as \( |a| \), is defined as follows: $$ |a| = \begin{cases} a & \text{if } a \geq 0 \\ \\ -a & \text{if } a < 0 \end{cases} $$
- If the number is positive or zero, its absolute value is simply the number itself.
- If the number is negative, its absolute value is the positive version of that number.
This definition tells us that the absolute value of any number is always positive or zero; it can never be negative.
Here are some examples to make this clearer.
The absolute value of a positive number is the number itself.
$$ |+3| = +3 $$
The absolute value of zero is zero.
$$ |0| = 0 $$
The absolute value of a negative number is its positive counterpart.
$$ |-2| = +2 $$
In other words, for a negative number, just flip the sign to get its absolute value.
A Geometric Perspective
To get a better sense of this concept, think of absolute value as the distance between a number and zero on a number line.
Imagine a number line where each point represents an integer, with the center point, or origin, representing zero.
The absolute value of \( -2 \) is \( 2 \) because the point \( -2 \) lies 2 units away from the origin.
The absolute value of \( +3 \) is \( 3 \), as the point \( +3 \) is 3 units from the origin.
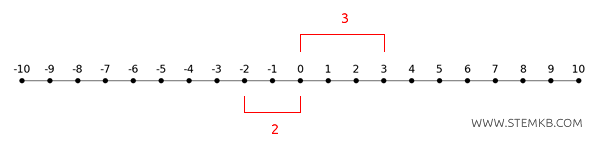
In both cases, you can see that absolute value ignores the sign and considers only the distance from zero.
Thus, absolute value measures a number's size without regard to direction, focusing solely on its magnitude.
The idea of absolute value is highly useful in many areas of mathematics and applied science, especially when the size of a value matters more than its sign. For example, in calculating distances between points on a line or in three-dimensional space, absolute value is essential for ensuring results are always positive.

