Co-prime or Relatively Prime Numbers

When we talk about relatively prime numbers (or co-primes), we’re referring to two or more natural numbers that share no common factors other than 1.

This means the greatest common divisor (GCD) of these numbers is 1.

In other words, there’s no number, other than 1, that can evenly divide both.

An Example

For instance, the numbers 12 and 13 are co-prime because they have no common factors (apart from 1).

$$ GCD(12,13)=1 $$

Conversely, 12 and 15 are not co-prime, as they both share 3 as a factor.

$$ GCD(12,15)=3 $$

To determine if two numbers are co-prime, you can use the greatest common divisor (GCD) method known as Euclid’s algorithm.

How Euclid’s Algorithm Works

Euclid’s algorithm is one of the most efficient ways to find the GCD. It works through a sequence of divisions until one of the numbers reduces to zero.

To calculate the GCD of two numbers \( a \) and \( b \) :

1. Divide the larger number by the smaller one, and find the remainder.
2. Replace the larger number with the smaller one, and the smaller one with the remainder from the last step.
3. Repeat this process until the remainder is zero.

When the remainder is zero, the last divisor used is the GCD of the original two numbers.

If the GCD is 1, the numbers are co-prime.

Example

Let’s take 12 and 13 and check if they’re co-prime:

1. Divide 13 by 12, getting a quotient of 1 and a remainder of 1.
2. Replace 13 with 12, and 12 with 1.
3. Divide 12 by 1, obtaining a remainder of 0.

Since the remainder is now zero, the last divisor used is 1, which is the GCD.

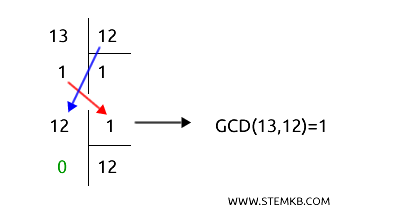
This confirms that 12 and 13 are co-prime.

Example 2

Now, try this with 12 and 15:

1. Divide 15 by 12, yielding a quotient of 1 and a remainder of 3.
2. Replace 15 with 12, and 12 with 3.
3. Divide 12 by 3, yielding a remainder of 0.

In this case, the last divisor is 3, so the GCD of 12 and 15 is 3.

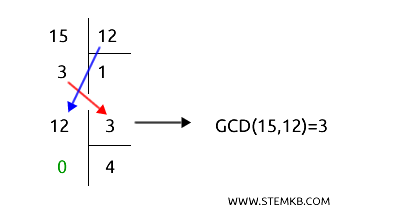
Since the GCD is not 1, this means that 12 and 15 are not co-prime, as they have a common factor.