Greatest Common Divisor

The greatest common divisor (GCD) of two or more non-zero numbers, $a$ and $b$, is defined as the largest number that divides both without leaving a remainder. $$ G.C.D.(a, b) $$ In other words, it’s the greatest number that divides both $a$ and $b$ perfectly.

To make the concept of the greatest common divisor (GCD) clearer, let’s walk through a practical example.

Example

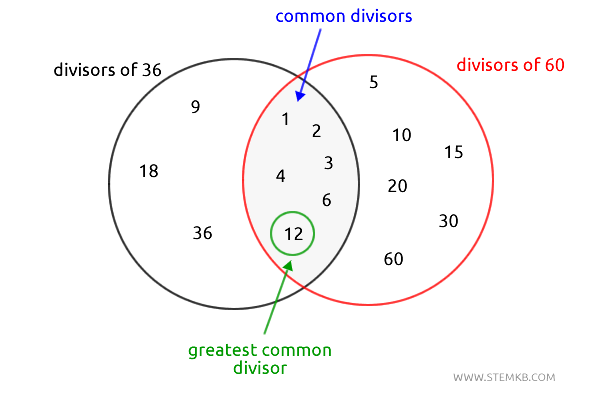
We need to find the greatest common divisor of 36 and 60—that is, the largest number that divides both values.

First, let’s list all the divisors of 36, meaning the numbers that divide 36 without a remainder:

$$ 1, 2, 3, 4, 6, 9, 12, 18, 36 $$

Next, we list the divisors of 60:

$$ 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 $$

Now, let’s find the numbers that both lists have in common:

$$ 1, 2, 3, 4, 6, 12 $$

Among these shared divisors, the largest is 12.

This tells us that 12 is the greatest common divisor of 36 and 60.

example

We can write:

$$ G.C.D.(36, 60) = 12 $$

Both 36 and 60 are divisible by 12, and it’s the largest divisor they share.

In the next section, we’ll explore other methods for finding the greatest common divisor.

Methods for Finding the G.C.D.
Why Is Knowing the Greatest Common Divisor Useful?
The Connection Between the Greatest Common Divisor and the Least Common Multiple

Methods for Finding the G.C.D.

There are various methods for determining the greatest common divisor, such as:

Prime Factorization
This method involves breaking down each number into its prime factors, then multiplying only the common factors with the lowest exponents.
Example. Let’s find the greatest common divisor of 36 and 60 using the prime factorization method. Start by breaking down 36 into its prime factors: $$ 36 = 2^2 \times 3^2 $$ Next, break down 60: $$ 60 = 2^2 \times 3^1 \times 5^1 $$ Now, to find the G.C.D., take only the common prime factors with the smallest exponents ($ 2^2 $ and $ 3^1 $). So, the product of these shared factors is: $$ G.C.D.(36, 60) = 2^2 \times 3^1 = 4 \times 3 = 12 $$ Thus, the greatest common divisor of 36 and 60 is 12, which matches the result we found earlier.
Euclidean Algorithm
This efficient method finds the G.C.D. through successive division. The process involves dividing until there’s a remainder of zero, at which point the last non-zero divisor is the G.C.D. This method is particularly useful for large numbers.
Example. Let’s use the Euclidean algorithm to find the G.C.D. of 36 and 60. Begin with 60 and 36, dividing the larger number by the smaller: $$ 60 \div 36 = 1 \text{ with remainder } 24 $$ Now divide 36 by 24. $$ 36 \div 24 = 1 \text{ with remainder } 12 $$ Finally, divide 24 by 12: $$ 24 \div 12 = 2 \text{ with remainder } 0 $$ When you reach a remainder of zero, the last non-zero divisor (in this case, 12) is the G.C.D. of the initial numbers. So, the G.C.D. of 36 and 60, calculated via the Euclidean algorithm, is: $$ G.C.D.(36, 60) = 12 $$ This confirms the same result as before!

Why Is Knowing the Greatest Common Divisor Useful?

The greatest common divisor is fundamental in many areas of mathematics and its applications.

For example, it’s essential for reducing fractions.

Knowing the G.C.D. lets you simplify a fraction to its lowest terms.

Example. Consider the fraction $\frac{36}{60}$. We can simplify it by using the G.C.D. As we calculated earlier, the G.C.D. of 36 and 60 is 12. So, to reduce the fraction, divide both the numerator and denominator by 12: $$ \frac{36 \div 12}{60 \div 12} = \frac{3}{5} $$ The fraction $\frac{36}{60}$, reduced to its simplest form, is $\frac{3}{5}$. Working with simplified fractions makes calculations easier and clearer.

However, the uses of the G.C.D. go beyond this.

Beneath these simple ideas lie powerful mathematical tools.

For instance, the G.C.D. is used in studying the properties of integers and plays a crucial role in cryptographic algorithms, where it’s essential to understand prime numbers and their relationships.

So, understanding the G.C.D. is a step toward more advanced mathematics.

The Connection Between the Greatest Common Divisor and the Least Common Multiple

The link between the greatest common divisor (G.C.D.) and the least common multiple (L.C.M.) of two numbers $a$ and $b$ is expressed by the formula: $$ a \cdot b = G.C.D.(a, b) \cdot L.C.M.(a, b) $$

This means that if you already know the least common multiple of two numbers, you can also find the greatest common divisor using the following calculation:

$$ G.C.D.(a, b) = \frac{a \cdot b}{L.C.M.(a, b)} $$

The G.C.D. is found by multiplying the common factors raised to their lowest powers, while the L.C.M. is the product of all factors (both common and unique) raised to their highest powers. If $a$ and $b$ are coprime, their L.C.M. is simply $a \cdot b$. This relationship applies to any pair of integers, enabling you to calculate one value if you know the other and the product.

Example

Consider the numbers $a = 12$ and $b = 18$.

Start by finding the prime factorization of each:

$$ a = 12 = 2^2 \cdot 3 $$

$$ b = 18 = 2 \cdot 3^2 $$

To find the G.C.D., multiply the common factors with the lowest exponents:

$$ G.C.D.(12, 18) = 2 \cdot 3 = 6 $$

Then, calculate the L.C.M. by using all factors with their highest exponents:

$$ L.C.M.(12, 18) = 2^2 \cdot 3^2 = 36 $$

Now, let’s verify the relationship between the G.C.D. and the L.C.M.:

$$ a \cdot b = G.C.D.(a, b) \cdot L.C.M.(a, b) $$

$$ 12 \cdot 18 = 6 \cdot 36 $$

Both sides equal 216, confirming that $ a \cdot b = G.C.D.(a, b) \cdot L.C.M.(a, b) $.

Therefore, if you know the least common multiple of two numbers—such as $ L.C.M.(12, 18) = 36 $—you can indirectly find the greatest common divisor.

$$ G.C.D.(12, 18) = \frac{12 \cdot 18}{L.C.M.(12, 18)} = \frac{12 \cdot 18}{36} = \frac{18}{3} = 6 $$

This provides an alternative method for calculating the G.C.D.