Prime Numbers

Prime numbers are natural numbers greater than 1 that are only divisible by 1 and themselves.

For example, 23 is prime because its only divisors are 1 and 23.

Another prime number is 7, as it’s divisible only by 1 and 7.

Prime numbers have captivated mathematicians throughout the ages.

Beneath their apparent simplicity lie extraordinary properties. In fact, as early as 300 B.C., Euclid proved that there are infinitely many prime numbers: no matter how far you count, there will always be more primes yet to be discovered. Later, around 200 B.C., the Greek mathematician Eratosthenes developed an ingenious method for identifying prime numbers, known as the Sieve of Eratosthenes—a technique still in use today.

In contrast, a composite number can be broken down into prime factors; that is, it can be expressed as the product of primes.

For instance, 18 is composite because it can be written as \( 2 \times 3 \times 3 \), where both 2 and 3 are prime numbers.

This decomposition, called factorization, is a fundamental process in many algorithms and forms the backbone of cryptography.

The Infinity of Prime Numbers

The Greek mathematician Euclid elegantly demonstrated that there are infinitely many prime numbers.

Imagine you have a finite list of primes, for instance, 2, 3, 5, 7, all the way up to N.

Suppose, hypothetically, that N is the largest prime.

If you multiply all these primes together and add 1, you end up with a new number that can’t be divided evenly by any of the primes in our list; dividing by any of them will leave a remainder of 1.

$$ P = ( 2 \times 3 \times 5 \times 7 \times ... \times N ) + 1 $$

This new number \( P \) is evidently larger than \( N \).

$$ P > N $$

Now, two possibilities arise: either \( P \) is prime, or it is divisible by some prime not included in our initial list.

• If \( P \) is prime, then \( N \) isn’t the largest prime.
• If \( P \) isn’t prime, then it must be divisible by a prime outside our original list of 2, 3, 5, 7, ..., \( N \).

Either way, this shows that \( N \) cannot be the largest prime.

This conclusion proves the infinity of prime numbers.

The allure of prime numbers lies in their boundlessness and unpredictability, qualities that grant them a unique place in both mathematics and modern technology.

The Sieve of Eratosthenes

To find prime numbers up to a certain limit, Eratosthenes devised a method known as the Sieve of Eratosthenes.

Imagine listing the numbers from 2 up to a certain value, \( n=50 \).

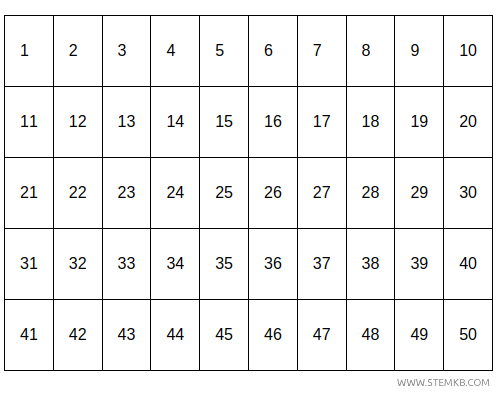
First, exclude the number 1, then eliminate every multiple of 2 (i.e., all even numbers except for 2 itself).

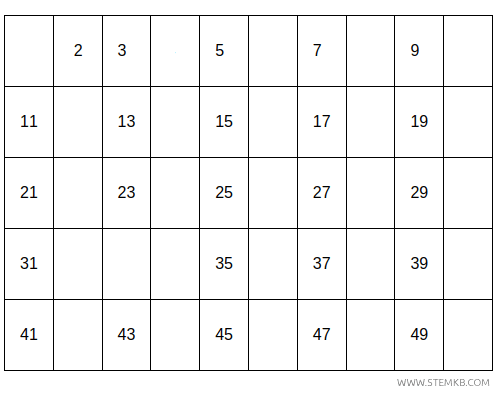
Next, eliminate every multiple of 3.

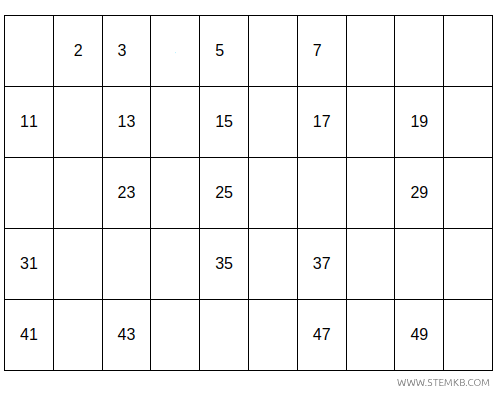
Then, every multiple of 5.

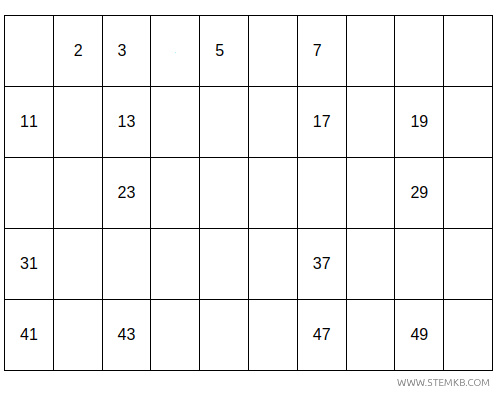
Then, every multiple of 7.

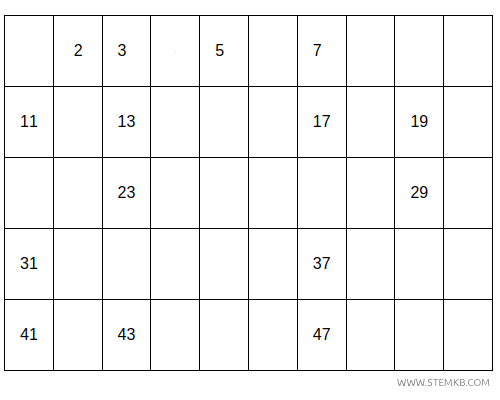
Finally, every multiple of 11.

At the end of this process, the numbers left are prime.

For example, applying the sieve up to 50 yields the primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47.

The insights of Euclid and Eratosthenes, which date back thousands of years, continue to be instrumental in unveiling these fundamental elements of our numerical world.

Primality Testing

To check if a number is prime without dividing by every smaller number, you can use a key principle: only check divisors up to the square root of the number.

For a number \( N \), if none of the primes up to \( \sqrt{N} \) divide \( N \) exactly, then \( N \) is prime.

For instance, to check if 157 is prime, it’s enough to verify that it isn’t divisible by any prime numbers less than or equal to \( \sqrt{157} \approx 12.5 \): namely, 2, 3, 5, 7, and 11.

• \( 157 \div 2 = 78, \ \text{remainder} = 1 \)
• \( 157 \div 3 = 52, \ \text{remainder} = 1 \)
• \( 157 \div 5 = 31, \ \text{remainder} = 2 \)
• \( 157 \div 7 = 22, \ \text{remainder} = 3 \)
• \( 157 \div 11 = 14, \ \text{remainder} = 3 \)

Since none of these primes divide 157, we can conclude that 157 is prime.

This means there’s no need to check for divisibility by primes greater than 11.

Consider the next prime after 11, which is 13. If you calculate \( 13 \times 13 = 169 \), you get a number larger than 157, so 13 can’t divide 157. The same reasoning applies to all primes greater than \( \sqrt{157} \approx 12.5 \).

The Significance of Prime Numbers in Mathematics and Cryptography

Prime numbers are essential in mathematics as the building blocks of integers: every composite number can be uniquely factored into prime numbers.

This property forms the foundation of modern cryptography, where data security relies on the difficulty of breaking large numbers into their prime factors, a task requiring immense computational resources.

In summary, while prime numbers may seem simple at first glance, they conceal a world of mystery and applications, from the basics of arithmetic to the cutting edge of cybersecurity.