
Symbolic Variables in Matlab
Today, we're going to talk about symbolic variables in Matlab.
What is a symbolic variable? A symbolic variable is a special kind of variable that only stores the symbol, such as "x", for use in calculations. It doesn't store a specific numerical value. This allows you to perform symbolic algebraic calculations with one or more unknowns, like solving equations with two or more variables, or adding two polynomials.
To define a symbolic variable, we use the syms function.
For example, you can define a symbolic variable "x" like this:
>> syms x
You can also define multiple symbolic variables at once by listing them one after the other, separated by spaces. For instance:
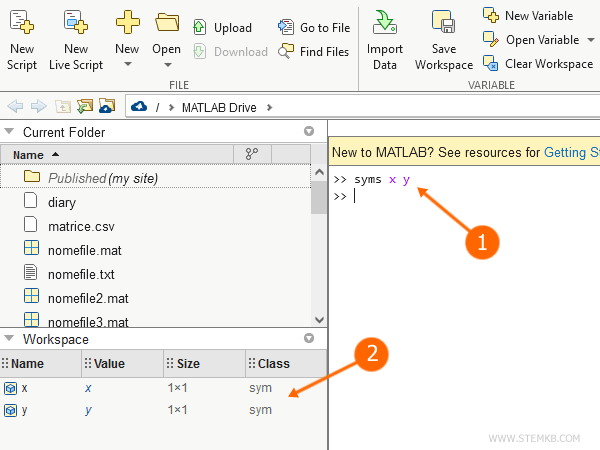
>> syms x y
Each time you declare a symbolic variable, you can see it in the workspace of Matlab.
Symbolic variables are associated with the "sym" class.
Now, let's do a practical example.
Suppose you have two polynomials:
$$ P(x) = 2x + y $$
$$ Q(x) = 4x - 2y $$
And you need to multiply them together.
$$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$
To perform this algebraic calculation in Matlab, you define the two symbolic variables "x" and "y" using the "syms x y" command:
>> syms x y
Then you type this expression, pq = (2x+y)(4x-2y), on the command line.
>> pq = (2*x+y)*(4*x-2*y)
ans =
(4*x - 2*y)*(2*x + y)
Matlab recognizes "x" and "y" as symbols and defines the symbolic expression.
In this case, Matlab doesn't substitute "x" and "y" with numbers but uses them as symbols of two unknown variables.
To perform the algebraic calculation, we use the expand(pq) function.
>> expand(pq)
ans =
8*x^2 - 2*y^2
Matlab performs the typical symbolic algebra calculation, returning the product of the two polynomials.
The result is the expression 8x2-2y2
Verify. To check if the result is correct, we multiply the two polynomials algebraically: $$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$ $$ P(x) \cdot Q(x) =2x \cdot 4x + 2x \cdot (-2y) + y \cdot 4x + y \cdot (-2y) $$ $$ P(x) \cdot Q(x) =8x^2 - 4xy + 4xy -2y^2 $$ $$ P(x) \cdot Q(x) =8x^2 -2y^2 $$ As you can see, the result is correct. That's all for today.

