
Limit of a Function Using Matlab
Today, let's delve into the fascinating world of function limits, exploiting the computational capabilities of Matlab. We'll not only understand the concept but also put it into practice with illustrative examples.
Before we set off, let's clear the air about what function limits are. A function limit is the value a function is progressively approaching as its independent variable inches towards a specific point. In layman's terms, it paints a picture of the function's behavior in the vicinity of that specific point.
Kick-off the process by introducing 'x', the independent variable, into the Matlab command line, using the 'syms' command.
syms x
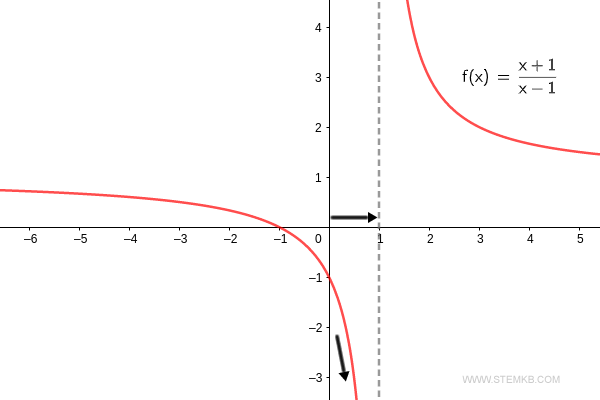
To get the ball rolling, let's work with the function f(x)=(x+1)/(x-1), where 'x' is our independent variable. We're aiming to find the limit as 'x' heads towards infinity.
$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$
You'll then need to input the 'limit()' command. Set the function f(x) as the first parameter, 'x' as the second, and 'Inf' (indicating positive infinity) as the third parameter. Once done, simply hit enter.
limit((x+1)/(x-1),x,Inf)
Voilà! Matlab swings into action and dutifully returns the limit of the function.
ans = (sym) 1
Lo and behold, the limit of the function as 'x' marches towards infinity is one.
But don't just take my word for it. As we can see, the limit of the function f(x)=(x+1)/(x-1) as 'x' heads to infinity is indeed one. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$ Our function's limit stands at one as 'x' takes a stroll towards infinity.
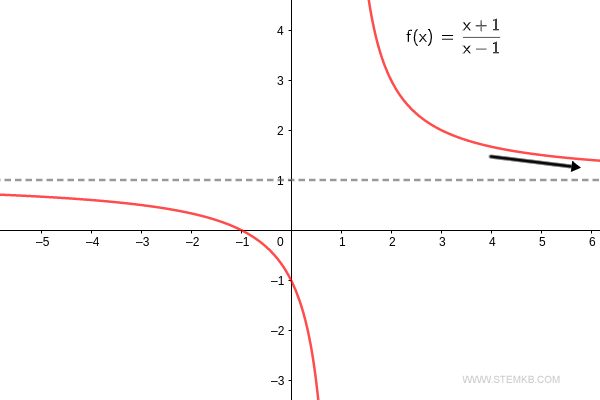
If you're curious about the limit as x→-∞, just add '-inf' as the third parameter to the command.
limit((x+1)/(x-1),x,-inf)
As 'x' nosedives towards negative infinity, the function does the opposite and climbs towards one.
ans = (sym) 1
Just to prove the point, the limit of the function f(x)=(x+1)/(x-1) for x→-∞ is a solid one. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$ You can check out the function's graph as it trails off towards negative infinity.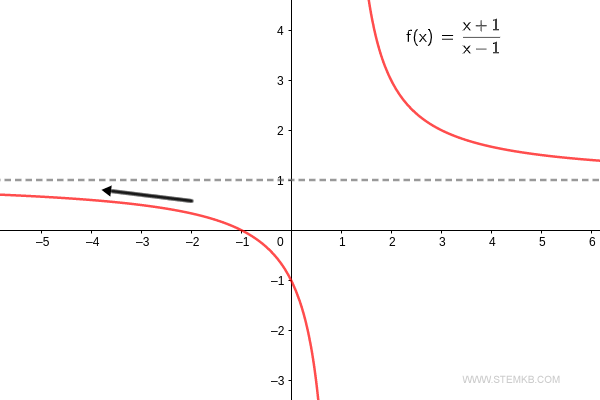
Should you wish to determine the function's limit at a specific accumulation point, 'x0', just insert the accumulation point as the third parameter.
For instance, let's say we're chasing the limit of the function as 'x' edges towards two.
limit((x+1)/(x-1),x,2)
Here, the limit shapes up to be three.
ans = (sym) 3
Checking our work, the limit of the function f(x)=(x+1)/(x-1) as x→2 lands at three. $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$ Thus, the function's limit pegs at 3 when 'x' veers towards 2.
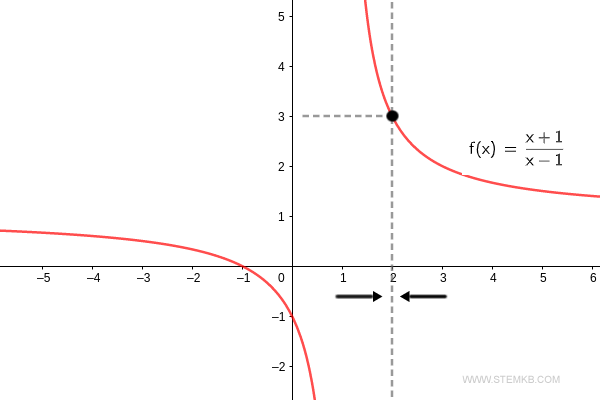
If you're only after the right-hand limit, add 'right' as the fourth argument in the same command.
limit((x+1)/(x-1),x,1,'right')
The result? The right-hand limit of the function as 'x' hones in on 1 is positive infinity ( ∞ ).
ans = (sym) ∞
Just to confirm, as the function f(x)=(x+1)/(x-1) nears x=1+ from the right, it shoots off to positive infinity. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$ So, the right-hand limit of the function skyrockets to infinity as 'x' homes in on one.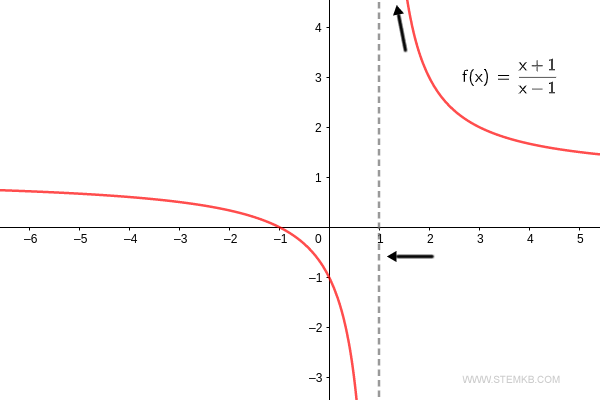
Alternatively, if the left-hand limit is your goal, simply add 'left' as the fourth parameter.
limit((x+1)/(x-1),x,1,'left')
And what do we find? The left-hand limit of the function as 'x' bears down on 1 plummets to negative infinity ( -∞ ).
ans = (sym) -∞
On checking, we see that the left-hand limit of the function f(x)=(x+1)/(x-1) for x→1- does indeed plummet to negative infinity. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$ And there we have it, the left-hand limit of the function freefalls to negative infinity as 'x' closes in on one.
With that, you're now well-versed in how to wield Matlab to compute function limits. Happy calculating!

