Definite Integrals in Matlab

In this lesson I'm going to explain to you how to compute the definite integral of a mathematical function on Matlab.

Now, what is a definite integral, you might ask? A definite integral allows you to calculate the area enclosed between a function f(x), also known as the integrand function, and the horizontal x-axis within a given interval (a, b). This is denoted using the notation $$ \int_a^b f(x) \ dx $$

To solve definite integrals, you can use two functions in Matlab. The first is the int() function.

The int() function

To compute the definite integral of a function, you can use the int() function in Matlab.

int(function, a, b)

This function has three parameters:

• The first parameter is the expression of the integrand function f(x)
• The second parameter is the lower bound of integration (a)
• The third parameter is the upper bound of integration (b)

Note. It's worth noting that the int() function is based on symbolic calculation. Therefore, before you write the expression for the integrand function, you must define the unknown variable as a symbol using the syms function.

Let me give you a practical example to illustrate this.

Consider the elementary integral

$$ \int_1^2 2x \ dx $$

In this case, the integrand function is f(x)=2x and the interval of integration is (1,2).

Firstly, you must define the symbol for the variable of integration (x) using the syms function.

syms x

Then, type in the int() command, with the expression 2*x as the first parameter.

Enter the lower bound 1 as the second parameter, and the upper bound 2 as the third parameter for the interval of integration (1,2).

int(2*x,1,2)

The result is the definite integral of 2x over the interval (1,2)

ans = 3

In this case, the definite integral is equal to 3.

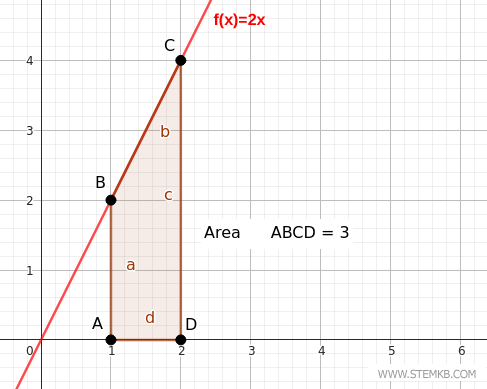
Verification. Now, to verify this, we can see that the definite integral of 2x over the interval (1,2) is very easy to calculate. The antiderivative of the function f(x)=2x is F(x)=x² $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$ If you look at the function on a Cartesian diagram, you can observe that the result of the definite integral ∫12 2x dx is the area enclosed between the graph of the function f(x)=2x and the x-axis within the interval (1,2).

The quad() function

Well, let's talk about this quad() function that we have here.

You see, to calculate the definite integral of a function, we can also use quad() in Matlab. It's quite simple, really.

We just call the function quad() with the integrand function, and the integration limits a and b, like this:

quad(function, a, b)

For instance, let's consider the integral from the previous paragraph: the integral from 1 to 2 of 2x dx.

$$ \int_1^2 2x \ dx $$

The integrand function is f(x)=2x and the integration interval is (1,2).

To evaluate this integral, we define an anonymous function f = @(x) 2*x

>> f = @(x) 2*x

Then we use quad(f,1,2) to calculate the definite integral over the integration interval from 1 to 2.

>> quad(f,1,2)

The quad() function estimates the area under the graph of the function f(x)=2x in the interval (1,2), and it returns the result, which in this case is 3. .

ans=3

Note. This is the same result we obtained in the previous example, where we solved the integral analytically using the fundamental theorem of calculus. $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$

What is the difference between the int and quad functions?

Now, you might be wondering what the difference is between the int() and quad() functions in Matlab.

In Matlab, the int() and quad() functions are used to calculate the definite integral of a function, but they are based on different methods.

• the int() function solves definite integrals of single-variable functions using numerical resolution methods such as the trapezoidal rule.
• the quad() function uses an adaptive quadrature method based on the Gauss-Kronrod algorithm. This method generally requires fewer calls to the function being integrated than other numerical methods, which makes it quite efficient.

So, that's a brief overview of how to calculate integrals using Matlab. It's a useful tool for engineers, physicists, and mathematicians alike.

With a little practice, you'll be able to use quad() and other numerical integration methods to solve all sorts of problems.