Extracting the diagonal of a matrix in Matlab

In this lesson, I will show you how to extract the elements of the diagonal of a matrix in Matlab.

What is the diagonal of a matrix? The main diagonal of a matrix is the set of elements that are located on the diagonal of the matrix starting from the top left element. For example, the main diagonal in this matrix are the elements 1, 5, 9 highlighted in red color. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Here's a practical example.

Create a square 3x3 matrix with three rows and three columns with these elements.

>> M=[1 2 3; 4 5 6; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

Now type the function diag(M) to extract the elements located on the main diagonal of the matrix.

>> diag(M)
ans =
1
5
9

The function extracts the elements on the main diagonal of the matrix.

In this case, they are the values 1, 5, and 9

$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

The diag() function allows you to extract other diagonals of the matrix.

For example, type diag(M,1) to extract the elements on the diagonal above the main diagonal.

>> diag(M,1)
ans =
2
6

In this case, the function diag(M,1) extracts the numbers 2 and 6 that are located on the diagonal above the main diagonal.

$$ M = \begin{pmatrix} 1 & \color{red}2 & 3 \\ 4 & 5 & \color{red}6 \\ 7 & 8 & 9 \end{pmatrix} $$

Now type the function diag(M,2)

>> diag(M,2)
ans = 3

This last command extracts the elements on the diagonal above the previous one...and so on.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$

If you want to extract diagonals below the main diagonal, indicate a negative integer as the second parameter.

For example, type diag(M,-1) to extract the elements of the diagonal below the main diagonal of the matrix.

>> diag(M,-1)
ans =
4
8

The function diag(M,-1) extracts the elements located below the main diagonal of the matrix.

$$ M = \begin{pmatrix} 1 & 2 & 3 \\ \color{red}4 & 5 & 6 \\ 7 & \color{red}8 & 9 \end{pmatrix} $$

If you want to eliminate all other elements of the matrix, leaving only those on the main diagonal, type diag(diag(M))

>> diag(diag(M))
ans =
Diagonal Matrix
1 0 0
0 5 0
0 0 9

This way, you get a diagonal matrix.

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \end{pmatrix} $$

How do you extract the secondary diagonal?

The secondary diagonal (or antidiagonal) is the diagonal of the elements of the matrix taken from right to left starting from the last element in the top right corner.

In the case of the 3x3 matrix in the previous example, the secondary diagonal is composed of the elements 3, 5, 7.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$

To extract the secondary diagonal of the matrix, you need to flip it horizontally using the function fliplr().

For example, type the command diag(fliplr(M))

>> diag(fliplr(M))
ans =
3
5
7

The function diag(fliplr(M)) extracts the elements on the secondary diagonal of the matrix.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$

Note.In this case, you can also use the second parameter of the function to extract diagonals above or below the main diagonal. To extract those above the secondary diagonal, enter a positive integer. For example, diag(fliplr(M),1) extracts the elements 2 and 4 just above the main diagonal. $$ M = \begin{pmatrix} 1 & \color{red}2 & \color{green}3 \\ \color{red}4 & \color{green}5 & 6 \\ \color{green}7 & 8 & 9 \end{pmatrix} $$ To extract diagonals below the secondary diagonal, enter a negative integer. For example, diag(fliplr(M),-1) extracts the elements 6 and 8 just below the main diagonal.
$$ M = \begin{pmatrix} 1 & 2 & \color{green}3 \\ 4 & \color{green}5 & \color{red}6 \\ \color{green}7 & \color{red}8 & 9 \end{pmatrix} $$ .

The diag() function allows you to extract elements on diagonals even from a rectangular matrix.

For example, create a 3x4 rectangular matrix with 3 rows and 4 columns.

>> M2=[1 1 1 1 ; 2 2 2 2 ; 3 3 3 3]
M2 =
1 1 1 1
2 2 2 2
3 3 3 3

Then type the command diag(M2)

>> diag(M2)
ans =
1
2
3

The command diag(M2) extracts the elements on the diagonal from left to right starting from the top left element.

$$ M = \begin{pmatrix} \color{red}1 & 1 & 1 & 1 \\ 2 & \color{red}2 & 2 & 2 \\ 3 & 3 & \color{red}3 & 3 \end{pmatrix} $$

In this way, you can extract any diagonal even if the matrix is not a square matrix.

Note. Even for rectangular matrices, you can extract the diagonals above or below the main diagonal by indicating a positive or negative integer as the second parameter. For example, type diag(M2,1) or diag(M2,-1) for the diagonals above and below the main diagonal, respectively. Similarly, type diag(M2,2) or diag(M2,-2) for the subsequent diagonals.

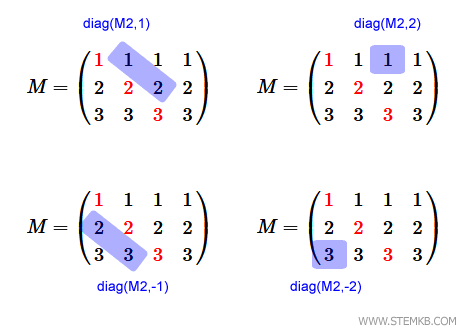
To extract the secondary diagonals from a rectangular matrix, you need to flip the matrix from right to left. For example, to extract the secondary diagonal, type diag(fliplr(M2)). In this case, the secondary diagonal starts from the upper rightmost element of the rectangular matrix. $$ M = \begin{pmatrix} 1 & 1 & 1 & \color{red}1 \\ 2 & 2 & \color{red}2 & 2 \\ 3 & \color{red}3 & 3 & 3 \end{pmatrix} $$