Linear Equations System in Matlab

In this Matlab lesson, I'll show you how to solve a system of linear equations using matrix and vector calculations.

Here's a practical example.

This linear equations system has two unknowns in two equations.

$$ \begin{cases} x+5y-3 = 0 \\ \\ 2x-4y+8=0 \end{cases} $$

Note. Equations are called linear when the highest degree of the unknowns is equal to 1.

Rewrite the equation system in the normal form ax+by=c.

Move the constant terms to the right-hand side, leaving the unknowns and their coefficients on the left-hand side of the equations.

$$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$

Now, convert the equation system into vector form.

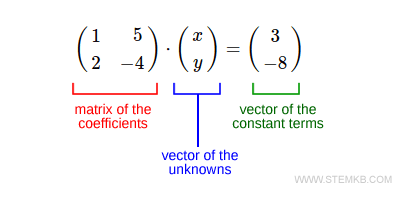
$$ \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$

The left matrix is the matrix of the coefficients of the unknown variables x and y.

$$ A = \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} $$

The first vector is the vector of the unknowns.

$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} $$

The last vector is the vector of the constant terms of the two equations.

$$ \vec{b} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$

Now let's see how to transform this information into variables in the Matlab working environment.

To define the coefficient matrix in Matlab, create a two-dimensional array.

Type A = [1, 5; 2, -4] on the command line.

>> A = [ 1 , 5 ; 2 , -4 ]
A =
1 5
2 -4

To define the constant terms vector in Matlab, create a one-dimensional array.

Type b = [3; -8]

>> b = [ 3 ; -8 ]
b =
3
-8

The equation system in vector form is the product of a matrix by a vector.

$$ A \cdot \vec{x} = \vec{b} $$

To find the solutions of the equation system, obtain the vector x by moving everything else to the right-hand side.

$$ \vec{x} = A^{-1} \cdot \vec{b} $$

The symbol A^-1 is the inverse matrix of the coefficient matrix A of the equation system.

At this point, calculate A^-1·b on Matlab by typing the command inv(B)*b

>> inv(A)*b
ans =
-2
1

The result is the values of x and y of the unknowns vector.

$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \end{pmatrix} $$

In this way, you have found the solution of the equation system.

$$ x=-2 $$

$$ y=1 $$

The linear equations system has a solution (x;y)=(-2;1).

Check if the solution is correct. Substitute the values x=-2 and y=1 in the initial equation system. Then carry out the algebraic calculations. $$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$ $$ \begin{cases} -2 + 5 \cdot 1 =3 \\ \\ 2 \cdot (-2) -4 \cdot 1 =-8 \end{cases} $$ $$ \begin{cases} 3 =3 \\ \\ -8 =-8 \end{cases} $$ All equations of the system are satisfied. Therefore, the solution x=-2 and y=1 is correct.