Rotating a Matrix in Matlab

In this lesson, I'll show you how to rotate a matrix or an array in Matlab.

What does rotating a matrix mean? The rotation operation turns the matrix clockwise (to the right) or counterclockwise (to the left). For example, a 90-degree clockwise rotation transforms a 2x3 matrix into a 3x2 matrix, where the first and second rows become the second and first columns, respectively.

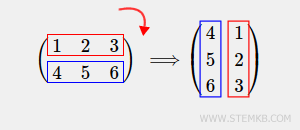
Here's a practical example.

Create a 2x3 rectangular matrix with two rows and three columns.

>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6

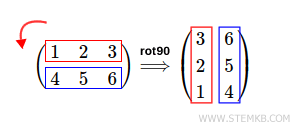
Then type the command rot90(M,1) to rotate the matrix 90 degrees counterclockwise.

>> rot90(M,1)
ans =
3 6
2 5
1 4

Matlab rotates the matrix 90 degrees counterclockwise.

Note. Alternatively, you can get the same rotation by typing rot90(M) because Matlab considers the second parameter to be 1 by default. The default direction is counterclockwise because it's the direction adopted in mathematics and physics.

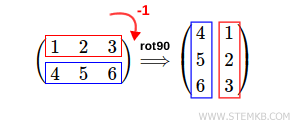
To rotate the matrix clockwise, i.e., clockwise, enter a negative value in the second parameter of the rot90() function.

For example, type rot90(M,-1) to get a 90-degree clockwise rotation of the matrix.

>> rot90(M,-1)
ans =
4 1
5 2
6 3

In this case, Matlab performs a 90-degree clockwise rotation of the matrix.

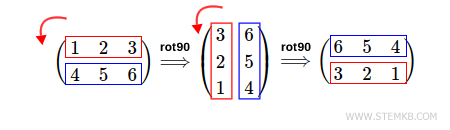
To rotate the matrix 180 degrees counterclockwise, type rot90(M,2)

>> rot90(M,2)
ans =
6 5 4
3 2 1

In this case, Matlab performs two 90-degree counterclockwise rotations of the matrix.

To rotate the matrix 180 degrees clockwise, type rot90(M,-2)

>> rot90(M,-2)
ans =
6 5 4
3 2 1

Matlab performs two 90-degree clockwise rotations of the matrix because the second parameter is a negative integer, i.e., -2.

Obviously, the final result is the same as the previous example: a 180-degree rotation.

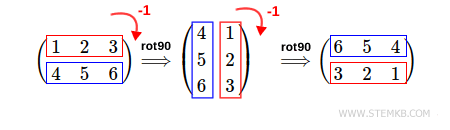
In practice, the rot90(M,n) function allows you to perform any number of 90-degree rotations.

The second parameter (n) of the function is the number of rotations counterclockwise (n>0) or clockwise (n<0).

For example, to rotate the matrix 270 degrees counterclockwise, type rot90(M,3).

>> rot90(M,3)
ans =
4 1
5 2
6 3

Matlab performs three 90-degree counterclockwise rotations of the matrix.

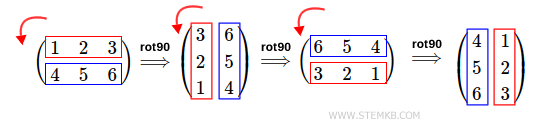
Note. To get a 270-degree clockwise rotation, simply type rot90(M,-3) by specifying the negative integer -3 as the second parameter of the "rot90()" function.

To perform a 360-degree counterclockwise rotation, type rot90(M,4)

>> rot90(M,4)
ans =
1 2 3
4 5 6

When you rotate 360 degrees, it doesn't matter if the rotation is counterclockwise (4), clockwise (-4), or zero (0).

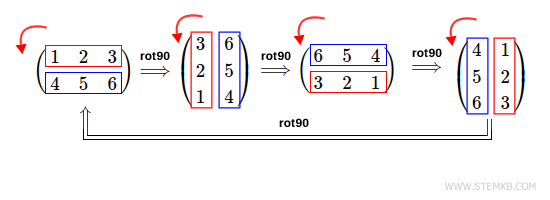
In both cases, the result is always the same.