Sparse Matrix in Matlab

In this online lesson, I'll explain how to create sparse matrices using Matlab.

What is a sparse matrix? Sparse matrices allow you to generate very large matrices while occupying less computer memory. For example, if you create a matrix with many constant values (e.g., zero), you repeat the same values in multiple elements, unnecessarily occupying a large part of memory. $$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ To reduce the amount of occupied memory, you can generate the same matrix as a sparse matrix, where the data is compressed because null values are ignored.

In Matlab, you can use sparse matrices to create compressed identity and diagonal matrices.

Sparse identity matrix

Let me give you a practical example.

Create an identity matrix using the eye(4) function

>> eye(4)
ans =
Diagonal Matrix
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

There are 12 zeros and 4 ones in the matrix. So, most of the space in the matrix (12 out of 16 elements) is unnecessarily occupied by zero.

Now create the same identity matrix using the technique of sparse matrices through the command speye(4).

>> speye(4)
ans =
Compressed Column Sparse (rows = 4, cols = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

In the sparse Matlab matrix, only the positions (row, column) of the matrix where there are non-zero values are listed, occupying a smaller amount of memory.

For this reason, it's called a "sparse" matrix.

Note that the sparse matrix occupies less memory because it considers only the useful information. In an identity matrix, zeros are insignificant elements in matrix calculation, so they are removed. This reduces the space occupied in memory (spatial complexity) and reduces the execution time of calculations (temporal complexity).

You can use the sparse matrix you just created in calculations as if it were a normal matrix.

For example, create a square matrix M with four rows and four columns.

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Then multiply matrix M by an identity matrix of size 4.

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Now multiply the same matrix M by a sparse identity matrix of size 4.

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

As you can see, the final result of the operations M*eye(4) and M*speye(4) is always the same.

However, in the operation with the sparse matrix M*speye(4), you obtained the result faster, using a smaller amount of computer memory.

Sparse diagonal matrix

In Matlab, there is a specific function to create sparse diagonal matrices. This function is called spdiags().

spdiags(v,i,r,c)

• The first parameter (v) is a column vector with the elements to be placed on the diagonal
• The second parameter (i) is the index of the diagonal where you want to place the elements. By default, it is 0 where zero is the main diagonal)
• The third (r) and fourth (c) parameters are the number of rows and columns of the sparse matrix to be created

For example, type spdiags([1;2;3],0,3,3) to create a sparse diagonal matrix of size 3x3.

>> spdiags([1;2;3],0,3,3)
ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 3 [33%])

(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

Matlab places the elements of the vector [1;2;3] on the main diagonal of a 3x3 matrix.

The resulting output is a sparse matrix of the diagonal matrix

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

How to manually create a sparse matrix

In Matlab, you can also define a sparse matrix by listing the position of each non-zero value in the matrix.

For example, create a sparse matrix based on this matrix

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Write the list of non-zero values of the matrix in an array, specifying the row, column, and value.

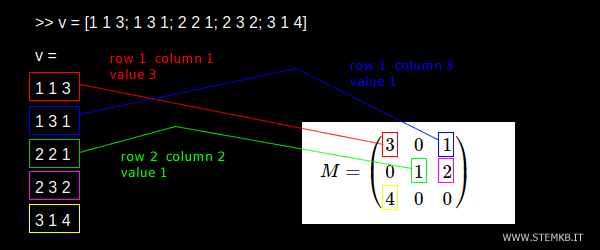
>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Each row of the array indicates the position (row and column) and a value of a non-zero element of the matrix.

The first non-zero element (3) of the matrix is located in the first row and first column (1,1). It is the element written in red in the example below. To indicate this element in the list of the sparse matrix, you need to write 1 1 3 in a row of the array. And so on.

Once you have defined the array with the list of non-zero values, create the sparse matrix using the spconvert() function.

>> spconvert(v)

The result is a sparse matrix with the values in the positions you indicated.

ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

When creating the array, you can define the non-zero elements of the matrix in any order.

You can also indicate the same position of the matrix multiple times using different values.

Please note that if you define the same position in the matrix multiple times in an array, Matlab will add all the values together. For example, if you create a sparse matrix indicating the value 2 and the value 3 at position (1,1), Matlab will consider the sum of the two values as 2+3=5 at position (1,1) in the matrix.

This method also allows you to generate a sparse matrix with complex numbers.