Matrices in Matlab

In this practical lesson, I will explain how to define a matrix using Matlab. You can create both square and rectangular matrices.

Let me give you a practical example.

Create a square 2x2 matrix with two rows and two columns.

$$ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

To define the matrix in Matlab, create an array variable and list the elements of the matrix within square brackets, separating the elements with spaces. For example: m = [1 2 3 4]

Then separate the rows of the matrix with semicolons (;).

Type m = [ 1 2 ; 3 4 ]

>> m = [ 1 2 ; 3 4 ]

Note. You can separate elements on the same row using spaces (m=[1 2;3 4]) or commas (m=[1,2;3,4]). The result is the same. I recommend separating elements with spaces as it makes it easier to see the semicolons that separate the rows. Additionally, using commas as separators can make the array less readable at a glance if the matrix elements are decimal numbers.

Matlab defines an array composed of two rows and two columns with the elements you indicated.

The result is the square 2x2 matrix

m =
1 2
3 4

After creating the matrix, you can use the array variable in any matrix calculation operation.

Esempio. For example, in Matlab, you can calculate the determinant of the matrix, the rank, the sum or product of two matrices, the inverse or transpose of a matrix, etc. For instance, to calculate the determinant of matrix m, type det(m).

Defining rectangular matrices in Matlab

To create a rectangular matrix, you can use the same procedure.

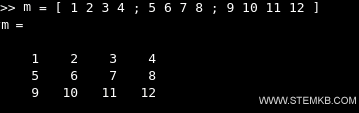
For example, define a 3x4 rectangular matrix with three rows and four columns:

$$ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{pmatrix} $$

To create the matrix in Matlab, write an array variable with 12 elements.

Separate the elements with spaces or commas. Then separate the rows with semicolons.

>> m = [ 1 2 3 4 ; 5 6 7 8 ; 9 10 11 12 ]

Matlab defines a two-dimensional array (rows and columns) composed of 12 elements arranged in three rows and four columns.

The result is the rectangular 3x4 matrix.

In this way, you can define any square or rectangular matrix with any number of rows and columns in two dimensions.