Calculating the Norm of a Vector in Matlab

In this lesson, I will explain how to calculate the norm (or magnitude) of a vector in Matlab.

What is the norm of a vector? It is the Euclidean length of the vector, also known as its magnitude. For example, the Euclidean norm of a vector in the plane is equal to the length of the arrow that represents it.
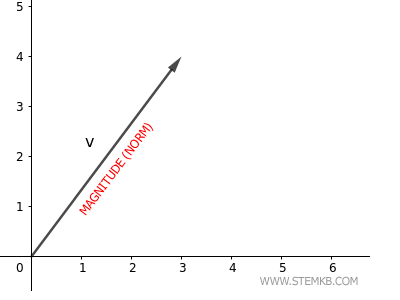
Vector Magnitude

Let me provide you with a practical example.

Consider a vector in the variable V

>> V=[3 4]
V =
3 4

This vector is applied to the origin (0;0) of the plane, with its endpoint at the point (3;4).

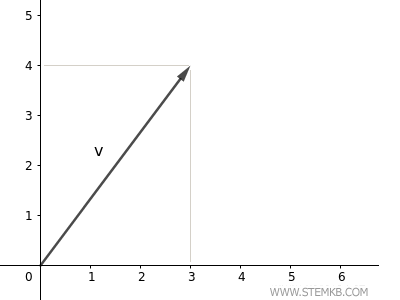
An example of a vector in the plane

To calculate the length of the vector (magnitude or norm), simply use the norm(V) function.

>> norm(V)
ans = 5

The Euclidean norm (magnitude) of the vector is 5.

It represents the length of the arrow that represents the vector on the plane.

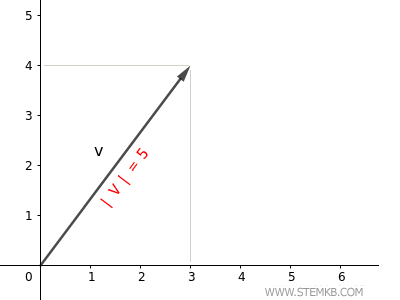
Vector Length

Verification. The length of a vector can also be calculated using the Pythagorean theorem $$ | \vec{v} | = \sqrt{3^2+4^2} = \sqrt{25} = 5 $$ The magnitude of the vector is indeed 5, which confirms the correctness of the result.