
Solving a system of linear equations in Matlab
Let me explain how to solve a system of linear equations in Matlab. It's all about matrix and vector calculations, you see.
Let me give you a practical example to illustrate.
Consider this system of two linear equations with two unknowns.
$$ \begin{cases} x+5y-3 = 0 \\ \\ 2x-4y+8=0 \end{cases} $$
Note that a system of equations is linear when the highest degree of the unknowns is 1.
We can rewrite the system in the standard form ax+by=c by moving the constants to the right-hand side and the variables to the left-hand side of each equation.
$$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$
Now, we can convert the system of equations into a vector form.
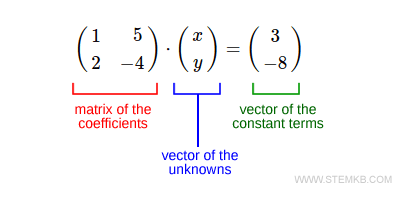
$$ \begin{pmatrix} 1 & 2 \\ 2 & -4 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$
The matrix on the left-hand side is the matrix of coefficients for the unknowns x and y.
$$ A = \begin{pmatrix} 1 & 2 \\ 2 & -4 \end{pmatrix} $$
The first vector is the vector of unknowns.
$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} $$
The last vector is the vector of constants from the equations.
$$ \vec{b} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$
Now, let's see how to transform this information into variables in the Matlab working environment.
To define the coefficient matrix in Matlab, we create a two-dimensional array by typing A = [1,2;2,-4] on the command line.
>> A = [ 1 , 2 ; 5 , -4 ]
A =
1 2
5 -4
To define the constant vector in Matlab, we create a one-dimensional array bt typing b = [ 3 ; -8 ]
>> b = [ 3 ; -8 ]
b =
3
-8
The equation system in vector form is the product of a matrix and a vector.
$$ A \cdot \vec{x} = \vec{b} $$
To find the solutions of the equation system, we solve for the vector x by moving everything else to the right-hand side.
$$ \vec{x} = A^{-1} \cdot \vec{b} $$
The symbol A-1 is the inverse matrix of the coefficient matrix A of the equation system.
To solve the system of equations, we need to find the inverse of the coefficient matrix A, which we can do in Matlab by typing inv(A), and then multiply it by the vector of constants b.
>> inv(A)*b
ans =
-2
1
The result will be the vector of unknowns x.
$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \end{pmatrix} $$
In this way, we have found the solution of the equation system.
$$ x=-2 $$
$$ y=1 $$
So, the solution to the system of equations is x=-2 and y=1.
Note. To verify that this solution is correct, we can substitute these values back into the original equations and check that they hold true. $$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$ $$ \begin{cases} -2 + 5 \cdot 1 =3 \\ \\ 2 \cdot (-2) -4 \cdot 1 =-8 \end{cases} $$ $$ \begin{cases} 3 =3 \\ \\ -8 =-8 \end{cases} $$ Well, you see, all the equations in the system are satisfied. Therefore, the solution x=-2 and y=1 is indeed correct.
Well, you see, it's all about manipulating matrices and vectors in Matlab. It's quite simple once you get the hang of it.

