Polynomials in Matlab

Let's talk about polynomials in Matlab.

What is a polynomial? Polynomials are just expressions that consist of constants and variables, or monomials, with integer exponents that are combined using basic arithmetic operations (addition, subtraction, multiplication, and division). or instance, this is a fourth-degree polynomial. $$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$ The degree of the polynomial is the highest exponent of the unknown variable x.

How to define a polynomial in Matlab

Now, to define a polynomial in Matlab, let's consider this example.

$$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$

The polynomial has only one unknown variable (x).

To use it in Matlab, you need to define a vector containing the numerical coefficients of the terms.

>> P = [1 2 -1 4 1]

The variable P is an array with the numerical coefficients of the polynomial P(x)=x⁴+2x³-x²+4x+1.

• The first element of the array is the coefficient 1 di x⁴
• The second element of the array is the coefficient 2 di 2x³
• The third element of the array is the coefficient -1 di -x²
• The fourth element of the array is the coefficient 4 di 4x
• The fifth element of the array is the coefficient 1 di +1

Once created, you can use it to compute the values of the polynomial P(x) by varying the variable x using the function polyval().

For example, to compute the value of the polynomial P(x) when x=0, type polyval(P,0)

>> polyval(P,0)

Matlab substitutes the value zero for the unknown x and returns the result.

In this case, the result is 1

ans = 1

Verify. You can quickly check by substituting x=0 in the polynomial $$ P(0) = x^4 + 2x^3 - x^2 + 4x +1 $$ $$ P(0) = (0)^4 + 2 \cdot 0^3 - 0^2 + 4 \cdot 0 +1 $$ $$ P(0)=1 $$ The result is 1.

Similarly, you can compute the value of the polynomial P(x) when x=1 by typing polyval(P,1)

>> polyval(P,1)

In this case, the result is 7

ans = 7

Verify. To verify the result, substitute x=1 in the polynomial $$ P(1) = x^4 + 2x^3 - x^2 + 4x +1 $$ $$ P(1) = (1)^4 + 2 \cdot 1^3 - 1^2 + 4 \cdot 1 +1 $$ $$ P(1)=1+2-1+4+1 $$ $$ P(1)=7 $$ The result is 7.

If you wish, you can also compute the value of the polynomial over a range of x values.

For instance, type x=0:5 to create an array x with the values from 0 to 5.

>> x=0:5
x =
0 1 2 3 4 5

Now calculate the values of the polynomial in the range from 0 to 5 using the function polyval(P,x)

>> polyval(P,x)

The function calculates the values of the polynomial for each element in the array x.

In this case, the result is an array composed of 6 elements.

ans =
1 7 37 139 385 871

Each element is the value of the polynomial in the interval (0,5).

Note. The first element of the array is P(0)=1 when x=0. The second element is P(1)=7 when x=1. The third element is P(2)=37. The fourth element is P(3)=139. And so on.

The use of arrays allows you to quickly perform any calculation.

Furthermore, they also allow you to graphically represent the polynomial on a Cartesian plane using the function plot().

For example, type these commands in sequence.

>> x=0:5;
>> P = [1 2 -1 4 1] ;
>> y=polyval(P,x);
>> plot(x,y);

The result is the graph of the polynomial in the interval (0,5).

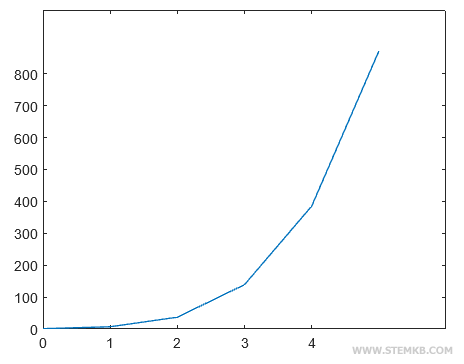
On the horizontal axis are measured the values of the unknown variable x, while on the vertical axis are those of the polynomial y.

Polynomial operations

You can use Matlab to perform operations with polynomials.

Let me give you a practical example.

Define the polynomial x³+2x²+3 in the array P1

>> P1 = [ 1 2 0 3 ]

Then define the polynomial 2x³-x²+3x+1 in the array P2

>> P2 = [ 2 -1 3 1 ]

Now perform these operations:

Addition

To add the two polynomials, type P1+P2

>> P1+P2
ans =
3 1 3 4

The result is the polynomial 3x³+x²+x+4

$$ P_1(x) + P_2(x) = (x^3+2x^2+3) + (2x^3-x^2+3x+1) $$ $$ P_1(x) + P_2(x) = x^3+ 2x^3+2x^2-x^2+3x+1+3 $$ $$ P_1(x) + P_2(x) = 3x^3+x^2+3x+4 $$

Subtraction

To calculate the difference between the polynomials, type P1-P2

>> P1-P2
ans =
-1 3 -3 2

The result is the polynomial -x³+3x²-3x+2

$$ P_1(x) - P_2(x) = (x^3+2x^2+3) - (2x^3-x^2+3x+1) $$ $$ P_1(x) - P_2(x) = x^3- 2x^3+2x^2+x^2-3x+1-3 $$ $$ P_1(x) + P_2(x) = -x^3+3x^2-3x-2 $$

Multiplication

To calculate the product between the polynomials P1·P2, you need to use the convolution function conv()

>> >> conv(P1,P2)
ans =
2 3 1 13 -1 9 3

The result is the polynomial 2x⁶+3x⁵+x⁴+13x³-x²+9x+3

$$ P_1(x) \cdot P_2(x) = (x^3+2x^2+3) \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = x^3 \cdot (2x^3-x^2+3x+1) + 2x^2 \cdot (2x^3-x^2+3x+1) + \\ \ \ + 3 \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = 2x^6-x^5+3x^4+x^3 + 4x^5-2x^4+6x^3+2x^2 + \\ \ \ + 6x^3-3x^2+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+(4x^5-x^5)+(3x^4-2x^4)+(x^3 +6x^3+ 6x^3) + \\ \ \ + (2x^2-3x^2)+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+3x^5+x^4+13x^3 -x^2+9x+3 $$

Division

To calculate the quotient of two polynomials, you need to use the deconvolution function deconv()

>> [q,r] = deconv(P1,P2)
q = 0.50000
r = 0.00000 2.50000 -1.50000 2.50000

The deconv() function returns two outputs:

• the quotient polynomial (q)
• the remainder polynomial (r)

The result is the quotient polynomial q=0,5

$$ Q = \frac{1}{2} $$

with remainder r=2,5x²-1,5x+2,5

$$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$

Verification. Carry out algebraic calculations to verify if the product is correct. $$ P_1(x) : P_2(x) = \frac{x^3+2x^2+3}{2x^3-x^2+3x+1} $$ In this case the calculation is a bit long.

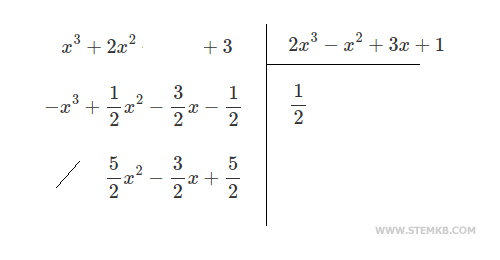
The quotient polynomial is $$ Q= \frac{1}{2} $$ con resto $$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ Multiply the quotient by the divisor polynomial and add the remainder: $$ Q \cdot (2x^3 -x^2+3x+1) + R $$ $$ \frac{1}{2} \cdot (2x^3 -x^2+3x+1) + \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 - \frac{1}{2} x^2+ \frac{3}{2}x+ \frac{1}{2}+ \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 + \frac{5-1}{2} x^2+ \frac{3-3}{2}x+ \frac{5+1}{2} $$ $$ x^3 + \frac{4}{2} x^2+ \frac{0}{2}x+ \frac{6}{2} $$ $$ x^3 + 2 x^2+ 3 $$ The result is the dividend polynomial. Therefore, the result of the division between the two polynomials is correct.