The rotation of a matrix in Octave

In this lesson I'll explain how to rotate a matrix in Octave with some practical examples.

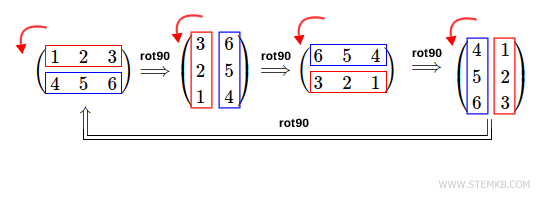
What is matrix rotation? The matrix rotates clockwise (to the right) or counterclockwise (to the left). For example if you rotate the matrix clockwise by 90 ° you get this result

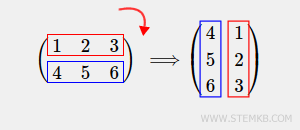
Make a 2x3 rectangular matrix

>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6

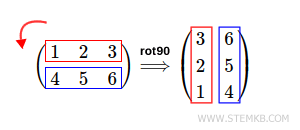
Now, rotate the matrix 90 ° counterclockwise.

Type rot90(M,1)

>> rot90(M,1)
ans =
3 6
2 5
1 4

The result is the 90 ° left rotation of the initial matrix.

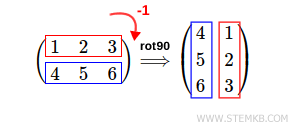
Note. To obtain this result you can also simply type rot90(M) because Octave defaults to the second parameter equal to 1. The default direction is counterclockwise (to the left) because it is the one commonly adopted in mathematics and physics. To rotate the matrix to the right you must, instead, indicate a negative number. For example -1.

If you want to rotate the matrix 90 ° to the right, type rot90 (M, -1)

In this case the second parameter is a negative integer that is -1.

>> rot90(M,-1)
ans =
4 1
5 2
6 3

This time the result is the matrix rotated 90 ° to the right.

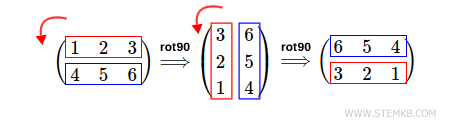
You can also rotate the matrix 180 ° to the left.

In this case you have to type rot90(M,2)

>> rot90(M,2)
ans =
6 5 4
3 2 1

The result is a double 90 ° rotation of the matrix to the left.

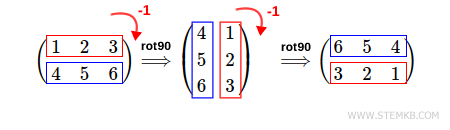
Similarly, you can rotate the matrix 180 ° to the right by typing rot90(M, -2)

In this case the second parameter is a negative integer that is -2.

>> rot90(M,-2)
ans =
6 5 4
3 2 1

The result is a double 90 ° rotation of the matrix to the right.

You can perform any number of rotations of the matrix using the rot90(M, n) function.

The second parameter indicates the number of rotations to the left (n> 0) or to the right (n <0).

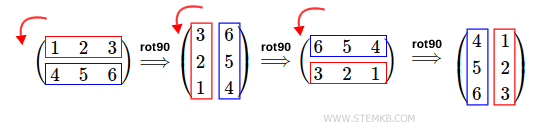
For example, to rotate the matrix 270 ° to the left, type rot90(M,3)

>> rot90(M,3)
ans =
4 1
5 2
6 3

The result is the matrix rotated three times 90 ° to the left

Note. To rotate the matrix 270 ° to the right you simply type rot90(M, -3) indicating -3 as the second parameter of the function.

To rotate the matrix 360 ° to the left, type rot90(M,4)

>> rot90(M,4)
ans =
1 2 3
4 5 6

In this case you get the same starting matrix because you have made four rotations of 90 ° to the left.