
The transpose of a matrix in Octave
In this lesson I'll explain how to transpose a matrix in Octave.
What is a transpose matrix? The transposition of a matrix consists in transforming each row into a column and vice versa. For example, the matrix M has two rows and three columns.
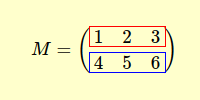
The transpose matrix MT is a matrix with the elements of each row in column.
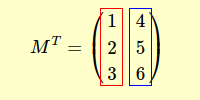
I'll give you a practical example
Make a rectangular matrix with six elements
>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6
The matrix has two rows and three columns.
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $$
To make the transpose matrix type the name of the variable followed by a quote M'
>> M'
ans =
1 4
2 5
3 6
Alternatively, you can also transpose the matrix by typing transpose(M)
>> transpose(M)
ans =
1 4
2 5
3 6
In both cases the result is the transpose matrix.
The transpose matrix is a 3x2 rectangular matrix with the rows arranged in a column
$$ M^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} $$
Note. The first row of the initial matrix was composed of the elements [1 2 3]. Now these elements are the first column of the transpose matrix. The same is true for the second row of the initial matrix. The second row [4 5 6] of the initial matrix is the second column of the transpose matrix.

