Graph Theory

At the heart of mathematics, graph theory delves into the intricate world of nodes—also known as vertices—and the connections between them, called edges.

Picture spreading several dots across a sheet of paper and drawing lines to connect some of them.

What emerges is a graph: a visual map illustrating how objects are interconnected.

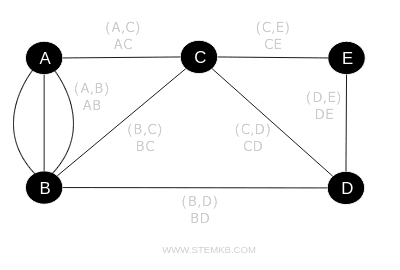
This remarkably adaptable concept has applications across a spectrum of fields, from biology and network technology to urban planning and computer science.

Graphs are distinguished by several features, including whether their edges are directed or undirected, if they include cycles (making them cyclic or acyclic), and their weight, should there be a value assigned to each edge.

Graph theory enables the solving of intricate problems such as identifying the most efficient path between two points, determining a graph's connectivity, or spotting smaller, recurring patterns within complex networks.

The real power of graph theory lies in its capacity to simplify and visually represent complex relationships, offering a means to analyze and solve challenges that might otherwise be daunting.

The Evolution of Graph Theory

Graph theory traces its origins back to the 18th century with the bridges of Königsberg problem, a puzzle presented by Leonhard Euler in 1736.

The city of Königsberg, nestled on the Pregel River in today's Kaliningrad, Russia, was famed for its seven bridges that connected different city sections.

 

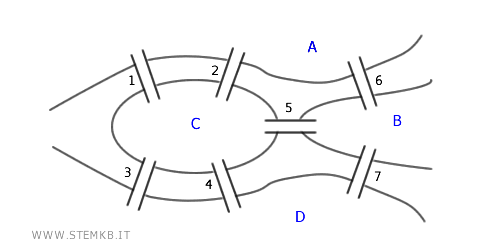
The posed question was both simple and provocative: Could one take a stroll, crossing each bridge exactly once, and return to the starting point?

Euler's proof that such a journey was impossible laid the groundwork for graph theory.

From these humble beginnings, graph theory has grown into an extensive and multidisciplinary field of mathematics.

In the 19th century, Gustav Kirchhoff applied graph theory to the study of electrical networks, setting the stage for future circuit analysis.

The 20th century saw a rapid expansion of the field, with algorithmic graph theory flourishing alongside the rise of computer science.

The advent of computing technology has enabled the analysis of graphs on a scale never before possible, finding applications in network science, optimization, and operations research, among others.

Today, graph theory stands as a cornerstone in diverse disciplines such as computational biology, sociology, and transportation engineering, demonstrating the enduring impact of a

Applications of Graph Theory

Graph theory finds its place in a multitude of disciplines, shining as a tool for elegantly mapping out complex relationships with simplicity and efficiency. Here are some significant areas where its impact is profound:

• Network Science: In social networking analysis, graphs peel back the layers of human connections, spotlighting influential figures, cohesive communities, and the veins of communication that run between them. This approach mirrors its utility in systems biology, where it illuminates the web of interactions between biological entities, such as networks of gene regulation or protein interactions.
• Route Optimization: From cracking the traveling salesman dilemma, navigating the quickest route through a maze of roads, to refining the arteries of transport and distribution networks, graph theory arms us with the critical tools needed to tackle these intricate optimization puzzles.
• Computer Science: Graph theory is the backbone of diverse aspects within computer science, from structuring data in graph-based databases, engineering search algorithms for the web, fortifying network security, to the conceptualization of hardware architectures.
• Game Theory and Economics: Graphs carve out the landscape of market models and game theory, sketching the interactions among economic agents or players to forecast the effects of strategic moves.
• Physical Sciences and Chemistry: The application of graphs stretches into the realm of molecular structure analysis and the prediction of chemical properties for new compounds. In physics, graph theory ventures into the domain of quantum mechanics, offering insights into the fundamental structure of our universe.
• Urban Planning and Transportation Engineering: Graphs offer a blueprint for deciphering transportation networks, enhancing traffic flow, guiding the development of new roadways, or sketching out the future of public transit systems.
• Telematics and Communications: When designing and optimizing telecommunication networks, graph theory is pivotal in ensuring these systems are not only efficient but resilient.

To sum up, graph theory's adaptability makes it an invaluable asset across virtually any field where decoding and understanding complex relationships is key.