Cycles in a Graph
A cycle within a graph represents a closed loop, a sequence of vertices where the journey begins and ends at the same point, with each successive pair of vertices linked by an edge.
Put simply, a cycle means traversing from one vertex back to itself without repeating any vertex along the way, except for the vertex where the loop both starts and ends.
Graphs can essentially be categorized into two groups when discussing cycles: undirected graphs and directed graphs (or digraphs).
- In undirected graphs, cycles are sequences of vertices connected in a loop by edges, where the final vertex leads back to the first. This loop is made without reusing any edges or vertices, with the exception of the starting/ending vertex.

- For directed graphs (digraphs), a cycle adheres to the same concept but considers the direction of the edges. Each edge must "point" towards the subsequent vertex in the sequence until it circles back to the starting point.
Cycles hold significance across a broad spectrum of applications, from optimizing networks and computer graphics to analyzing transport networks, scheduling systems, and even in identifying deadlocks within operating systems.
Identifying a cycle within a graph can be achieved through various algorithms, such as the Depth-First Search (DFS) algorithm, which flags a cycle if it encounters a previously visited vertex that isn't the immediate parent of the current vertex. Another notable cycle detection method is the Breadth-First Search (BFS).
The defining feature of a graph cycle is its ability to neatly arrange vertices in a continuous loop, forming a closed path where each vertex connects to the next, culminating in a return to the starting point.
Example
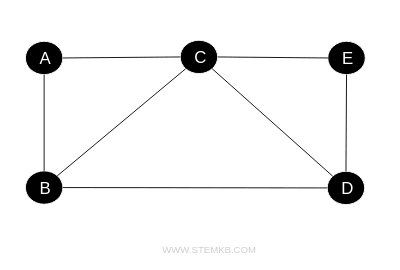
Consider a simple undirected graph depicted as follows:
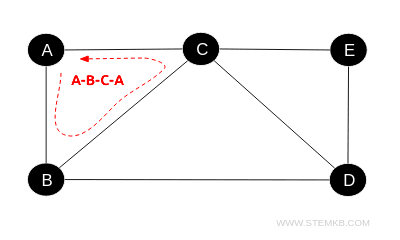
This graph showcases several cycles, such as the loop formed by the vertices A, B, C, and then back to A.

Such a cycle can be represented as the vertex sequence A-B-C-A or any cyclic permutation thereof (e.g., B-C-A-B).
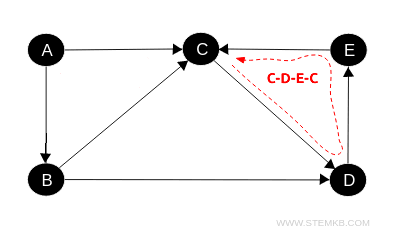
Another example includes the vertices B, C, D, returning back to B, and so forth.
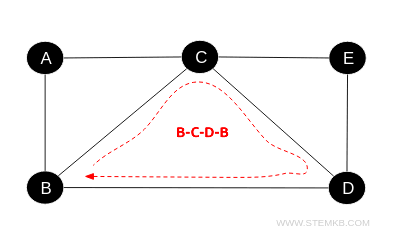
To unearth a cycle in this graph, one might deploy the Depth-First Search (DFS) algorithm. Here’s a streamlined explanation of how it operates:
- Starting at vertex A, we mark it as visited, noted in set V={A}.
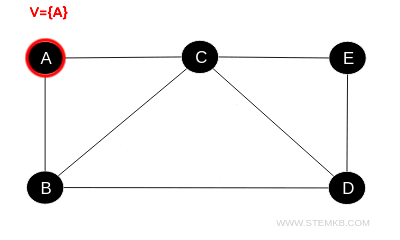
- Next, we move to an adjacent vertex, say B, mark it as visited, and continue, updating our visited set to V={A,B}.

- Moving from B to the adjacent C, not yet visited, we mark it and update our set to V={A,B,C}.
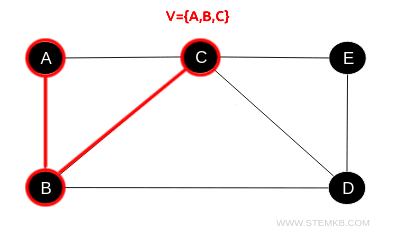
- Proceeding from C to A, we circle back to our starting point, which is already noted in our visited set V={A,B,C}, thus completing a cycle.
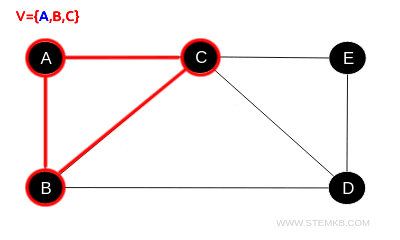
This illustration serves to demystify the concept of cycles in undirected graphs and the application of algorithms like DFS for their detection.
In scenarios of higher complexity, the foundational principles remain unchanged, though navigating through graphs with multiple cycles or avoiding the misidentification of cycles due to divergent visiting paths may introduce additional challenges.

