Number of Edges in a Graph

The number of edges that a simple graph can have depends on the number $ n $ of vertices.

In the worst-case scenario, a graph without cycles has $ n - 1 $ edges.

In the case with the most edges, a complete graph has $ \frac{1}{2}n(n - 1) $ edges.

A graph is called "simple" if it has no loops (edges connecting a vertex to itself) or multiple edges between two vertices. It is called "connected" if there is a path between every pair of vertices. It is called "complete" if every vertex is directly connected to every other vertex.

Any simple graph with $ n $ vertices and more than $ \frac{1}{2}(n - 1)(n - 2) $ edges is connected. This means there is a path between every pair of vertices in the graph.

The number of edges in a graph also depends on the number $ k $ of components.

A component of a graph is a subsection where every pair of vertices is connected by a path, and there are no connections between vertices of different components.

In other words, a component is a "piece" of the graph where you can travel from any vertex to any other vertex within that piece without leaving the component.

The number of edges $ m $ of a graph $ G $ with $ n $ vertices and $ k $ components is:

$$ n - k \le m \le \frac{1}{2}(n - k)(n - k + 1) $$

So, a graph with $ k $ components has at least $ n - k $ edges and at most $ \frac{1}{2}(n - k)(n - k + 1) $ edges.

Let's look at a practical example to clarify the theorem.

Example
Proof

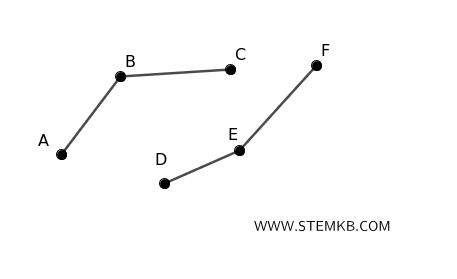
Example

Consider a simple graph with $ n = 6 $ vertices and $ k = 2 $ components.

The minimum number of edges it can have is $ n - k $.

$$ 6 - 2 = 4 $$

So, the graph must have at least 4 edges.

Imagine two components. The first component has 3 vertices (A, B, C), and the second component has 3 vertices (D, E, F). Each component is a tree (a connected graph without cycles) with 3 vertices, so each will have $ 3 - 1 = 2 $ edges. In total, the graph has $ 2 + 2 = 4 $ edges.
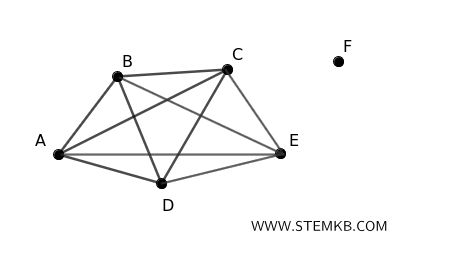
example

The maximum number of edges it can have is $ \frac{1}{2}(n - k)(n - k + 1) $.

$$ \frac{1}{2}(6 - 2)(6 - 2 + 1) = \frac{1}{2} \times 4 \times 5 = 10 $$

So, the graph can have a maximum of 10 edges.

Consider a graph with $ n = 6 $ vertices. We have a component (A, B, C, D, E) that forms a complete graph with $ 5 $ vertices and an isolated vertex F. The complete graph with 5 vertices contains $ \frac{1}{2} \times 5 \times 4 = 10 $ edges. Since vertex F is isolated, it does not contribute any additional edges to the graph. Consequently, a graph with $ n=6 $ vertices and $ k = 2 $ components can have a maximum of $ 10 $ edges.
example

If a graph with $ n = 6 $ vertices has more than $ \frac{1}{2}(n - 1)(n - 2) $ edges, then it is connected.

$$ \frac{1}{2}(6 - 1)(6 - 2) = \frac{1}{2} \times 5 \times 4 = 10 $$

So, a graph with more than 10 edges is necessarily connected.

To clarify this concept, consider a graph with $ n = 6 $ vertices (A, B, C, D, E, F) and 11 edges to see that it is connected.
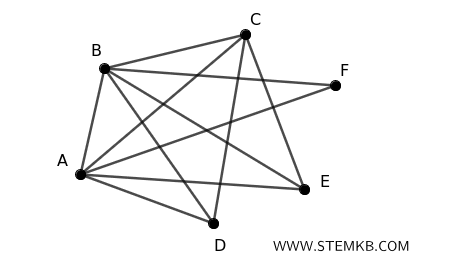
connected graph example
The maximum number of edges in a complete graph with 6 vertices is: $$ \frac{1}{2} \times 6 \times (6 - 1) = \frac{1}{2} \times 6 \times 5 = 15 $$ If a graph with 6 vertices has more than 10 edges, then it is connected. $$ \frac{1}{2}(6 - 1)(6 - 2) = \frac{1}{2} \times 5 \times 4 = 10 $$ In this case, the graph has 11 edges. We can see that every pair of vertices is connected, directly or indirectly, through a sequence of edges. Therefore, the graph is connected. This example confirms that if a graph with $ n = 6 $ vertices has more than 10 edges, it is necessarily connected, as the corollary states.

Proof

To prove the lower limit of edges, we use induction on the number of edges. The idea is that by removing an edge from a graph with the minimum number of edges, the number of components increases by 1.

From this, we demonstrate that the number of edges $ m $ must be at least $ n - k $.

To prove the upper limit of edges, we consider the case where each component of the graph is a complete graph (every vertex in the component is connected to every other vertex in the component).

The goal is to demonstrate that the maximum number of edges $ m $ in a graph $ G $ with $ n $ vertices and $ k $ components is $ \frac{1}{2}(n - k)(n - k + 1) $.

Suppose we have two components $ C_i $ and $ C_j $ with $ n_i $ and $ n_j $ vertices, respectively, where $ n_i, n_j > 1 $. In other words, we are looking at two complete subgraphs, each with more than one vertex.

Now, we replace $ C_i $ and $ C_j $ with new complete graphs that have $ n_i + 1 $ and $ n_j - 1 $ vertices, respectively.

By doing this, the total number of vertices in the graph $ G $ remains unchanged, but the number of edges changes.

The number of edges in a complete graph with $ n $ vertices is $ \frac{1}{2}n(n-1) $.

The number of edges in $ C_i $ with $ n_i $ vertices is $ \frac{1}{2}n_i(n_i - 1) $.
The number of edges in $ C_i $ after adding a vertex (becoming $ n_i + 1 $) is $ \frac{1}{2}(n_i + 1)n_i $.

The difference in the number of edges when $ C_i $ goes from $ n_i $ to $ n_i + 1 $ is:

$$ \frac{1}{2}(n_i + 1)n_i - \frac{1}{2}n_i(n_i - 1) $$

$$ \frac{1}{2}[n_i^2 + n_i - n_i^2 + n_i] = \frac{1}{2}(2n_i) = n_i $$

The number of edges in $ C_j $ with $ n_j $ vertices is $ \frac{1}{2}n_j(n_j - 1) $.

The number of edges in $ C_j $ after removing a vertex (becoming $ n_j - 1 $) is $ \frac{1}{2}(n_j - 1)(n_j - 2) $.

The difference in the number of edges when $ C_j $ goes from $ n_j $ to $ n_j - 1 $ is:

$$ \frac{1}{2}n_j(n_j - 1) - \frac{1}{2}(n_j - 1)(n_j - 2) $$

$$ \frac{1}{2}[n_j^2 - n_j - n_j^ 2 + 2n_j - 1] = \frac{1}{2}(2n_j - 1) = n_j - 1 $$

So, the total change in the number of edges when we replace the two components is:

$$ n_i - (n_j - 1) + 1 = n_i - n_j + 2 $$

This change is positive, meaning that increasing the number of vertices in one of the complete components and decreasing it in the other increases the number of edges.

To maximize the number of edges, each component must be as large as possible, which happens when there is one large component and the others are isolated vertices.

If we have $ k $ components, the largest component has $ n - k + 1 $ vertices (a complete graph), and the other $ k - 1 $ components are single isolated vertices.

The maximum number of edges is thus given by:

$$ \frac{1}{2}(n - k + 1)(n - k) $$

This leads to the theorem:

$$ m \le \frac{1}{2}(n - k)(n - k + 1) $$

If you have any further questions or if something specific is unclear, feel free to ask!