Bipartite Graphs
A bipartite graph stands out as a special type of graph in which vertices are split into two distinct independent sets. The rule is simple: every edge must connect a vertex from one set to a vertex from the opposite set, ensuring no edges exist between vertices within the same set.
This arrangement makes a graph bipartite if its vertices can be clearly divided into two unique groups, A and B, with the following characteristics:
- Distinct Groups
Vertex sets A and B are entirely separate, meaning a vertex belongs strictly to one set. - Inter-Group Connections Only
Edges exclusively bridge vertices from set A to set B and vice versa, with no intra-group connections.
These sets are commonly referred to as partition sets.
Consider a graph where the vertices {A,B,C} represent three employees, and {1,2,3} denote three distinct job openings.
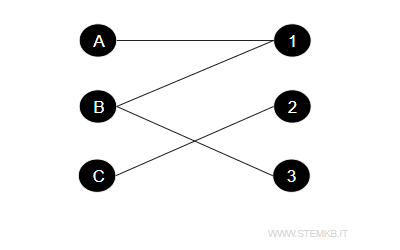
The edges symbolize the potential matches between employees and job openings, highlighting qualifications for specific positions.
In this illustration, it's clear that employee A fits job 1, employee B is suited for jobs 1 and 3, and employee C matches job 2.
This classic bipartite graph scenario shows no direct connections between individuals or jobs, maintaining a strict separation of categories.
A defining feature of bipartite graphs is the ability to color each vertex in such a way that no two connected vertices share the same color. Typically, two colors are used, often blue and red, to ensure that adjacent nodes are always distinguishable.
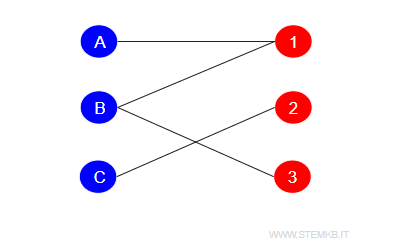
The implication here is that the graph's chromatic number—the least amount of colors needed to color the vertices while keeping adjacent ones different—is 2.
Such a coloring scheme is feasible only if the graph does not include any odd cycles, or cycles with an odd number of edges.
An odd cycle makes it impossible for a graph to be bipartite since coloring rules would inevitably lead to at least one pair of adjacent vertices sharing the same color.
For instance, adding a connection between 1 and 3 creates an odd cycle, which violates the coloring rule by having two adjacent vertices of the same color.
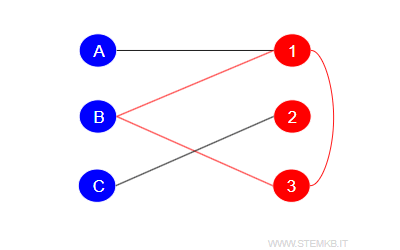
Therefore, a graph with odd cycles cannot qualify as bipartite.
On the other hand, bipartite graphs can accommodate even cycles—cycles with an even number of edges. Modifying the graph to introduce edges B-2 and C-3, for example, creates an even cycle that does not disrupt the bipartite structure.
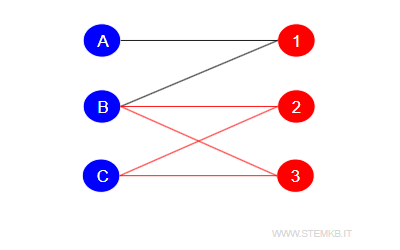
Thanks to this attribute, bipartite graphs are invaluable for scenarios that require avoiding direct matches or conflicts, such as in scheduling challenges or resource allocation tasks.
Complete Bipartite Graph
A complete bipartite graph (or biclique) is a specific type of bipartite graph where the vertices are divided into two disjoint sets \( U \) and \( V \), and every vertex in \( U \) is connected to every vertex in \( V \).
In other words, there are no edges between vertices within the same set, but each vertex in one set is connected to all vertices in the other set.
A complete bipartite graph is denoted as \( K_{r,s} \), where \( r \) and \( s \) are the number of vertices in sets \( U \) and \( V \) respectively. This means there are \( r \) vertices in set \( U \) and \( s \) vertices in set \( V \).
Overall, there are \( r \times s \) edges in the graph, since each vertex in \( U \) is connected to every vertex in \( V \).
For example, \( K_{3,2} \) is a complete bipartite graph with 3 vertices in one set and 2 vertices in the other set. Every vertex in the set with 3 vertices is connected to each of the 2 vertices in the other set, making a total of \( 3 \times 2 = 6 \) edges.
Here is a visual representation of \( K_{3,2} \):

In this example, each vertex in group \( U \) (1, 2, 3) is connected to each vertex in group \( V \) (4, 5). There are no edges between vertices within the same set.
Applications of Bipartite Graphs
Bipartite graphs are versatile tools with wide-ranging applications across various industries. Here are a few key uses:
They're instrumental in solving scheduling problems, playing a crucial role in matching algorithms that connect elements from two distinct sets.
For instance, they can help dodge scheduling conflicts in classroom planning or meeting room bookings.
Moreover, they're frequently employed to allocate tasks to machines, distinguishing tasks as one set and machines as another.
Characteristics of a Bipartite Graph
Key features and properties of bipartite graphs
- A graph G is bipartite if and only if every cycle in the graph is of even length
In a bipartite graph, each edge links a vertex from one set to a vertex in another disjoint set. Consequently, the graph can only contain cycles of even length.

